REPRESENTING PROPORTIONAL RELATIONSHIPS WITH EQUATIONS

Example 1 :

Meghan earns $12 an hour at her part-time job. Show that the relationship between the amount she earned and the number of hours she worked is a proportional relationship. Then write an equation for the relationship.

Solution :

Step 1 :

Make a table relating amount earned to number of hours.

Step 2 :

For each number of hours, write the relationship of the amount earned and the number of hours as a ratio in simplest form.

Amount earned : Number of hours

12 : 1 = 12 : 1

24 : 2 = 12 : 1

48 : 4 = 12 : 1

96 : 8 = 12 : 1

Since the ratios for the two quantities are all equal to 12:1, the relationship is proportional.

Step 3 :

Write an equation.

Let x represent the number of hours and y represent the amount earned.

Use the ratio as the constant of proportionality in the equation y = kx.

The equation is y = 12x/1 or y = 12x.

Example 2 :

In 1870, the French writer Jules Verne published 20,000 Leagues Under the Sea, one of the most popular science fiction novels ever written. One definition of a league is a unit of measure equaling 3 miles. Show that the relationship between miles and leagues is a proportional relationship. Then write an equation for the relationship.

Solution :

Step 1 :

Make a table relating amount earned to number of hours.

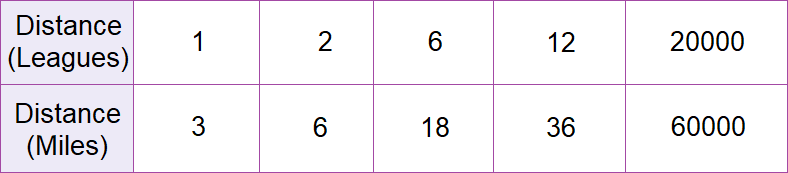
Step 2 :

For each number of league, write the relationship of the distance in miles and the distance in leagues as a ratio in simplest form.

Distance in miles : Distance in leagues

3 : 1 = 3 : 1

6 : 2 = 3 : 1

18 : 6 = 3 : 1

36 : 12 = 3 : 1

60,000 : 20,000  =  3 : 1

Since the ratios for the two quantities are all equal to 3:1, the relationship is proportional.

Step 3 :

Write an equation.

Let x represent the distance in leagues and and y represent the distance in miles.

Use the ratio as the constant of proportionality in the equation y = kx.

The equation is y = 3x/1 or y = 3x.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.