REPRESENTING COMPLEX NUMBERS IN ARGAND DIAGRAM

Question 1 :

Given the complex number z = 2 + 3i , represent the complex numbers in Argand diagram.

(i)  z, iz , and z + iz

Solution :

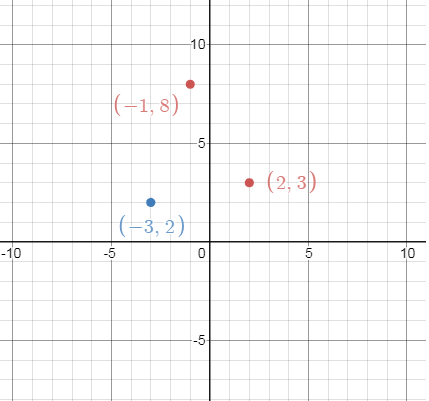
z = 2 + 3i

iz  =  i(2 + 3i)

  =  2i + 3i²

  =  2i + 3(-1)

iz  =  2i - 3

z + iz  =  (2 + 3i) + i(2 + 3i)

  =  2 + 3i + 2i + 3i² 

  =  2 + 3i + 2i + 3(-1) 

  =  2 + 3i + 2i - 3

  =  (2 - 3) + i(3 + 5)

z + zi  =  -1 + 8i

Set of ordered pairs of z is (2, 3) for iz is (-3, 2) and for z + zi is (8, -1).

(ii) z, − iz , and z − iz .

Solution :

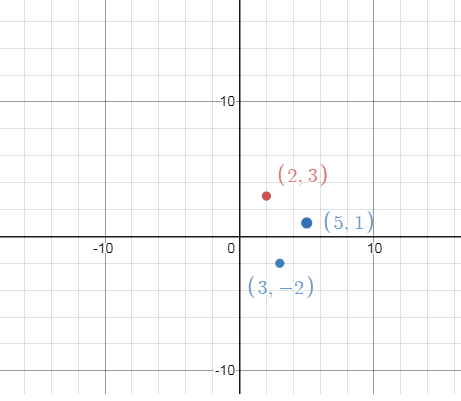
z = 2 + 3i

-iz  =  -i(2 + 3i)

  =  -2i - 3i²

  =  -2i - 3(-1)

-iz  =  -2i + 3

z - iz  =  (2 + 3i) - i(2 + 3i)

  =  2 + 3i - 2i - 3i² 

  =  2 + 3i - 2i - 3(-1) 

  =  2 - 2i + 3i + 3

  =  (2 + 3) + i(3 - 2)

  =  5 + i

z - zi  =  5 + i

Set of ordered pairs of z is (2, 3) for -iz is (3, -2) and for z - zi is (5, 1).

Solve for x and y in Complex Numbers

Question 1 :

Find the values of the real numbers x and y, if the complex numbers

(3− i)x − (2 − i) y + 2i + 5 and 2x + (−1+ 2i) y + 3+ 2i are equal

Solution :

(3− i)x − (2 − i) y + 2i + 5  =  2x + (−1 + 2i) y + 3+ 2i

3x - ix - 2y + iy + 2i + 5  =  2x - y + 2iy + 3 + 2i

(3x - 2y + 5) + i(-x + y + 2)  =  (2x - y + 3) + i(2y + 2)

Equating the real and imaginary values.

3x - 2y + 5  =  2x - y + 3 

3x - 2x - 2y + y  =  3 - 5

x - y  =  -2  ----(1)

-x + y + 2  =  2y + 2

-x + y - 2y  =  2 - 2

-x - y  =  0-----(2)

(1) + (2)

-2y  =  -2

y  =  1

By applying the value of y in (1), we get

x - 1  =  -2

x  =  -2 + 1

x  =  -1

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.