REPRESENTATION OF FUNCTIONS
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
A function may be represented by
(i) a set of ordered pairs
(ii) a table form
(iii) an arrow diagram
(iv) a graphical form
Let f : A --> B be a function.
(i) Set of ordered pairs :
The set f = {(x, y) | y ∈ f(x), x ∈ A} of all ordered pairs represent a function.
(ii) Table form :
The values of x and the values of their respective images under f can be given in the form of a table.
(iii) Arrow diagram :
An arrow diagram indicates the elements of the domain of f and their respective images by means of arrows.
(iv) A graph :
The ordered pairs in the collection
f = {(x,y) | y = f (x), x ∈ A}
are plotted as points in the xy- plane. The graph of f is the totality of all such points.
Every function can be represented by a curve in a graph. But not every curve drawn in a graph will represent a function.
Vertical line test will help us in determining whether a given curve is a function or not.
Vertical line test :
A curve drawn in a graph represents a function, if every vertical line intersects the curve in at most one point.
Example 1 :
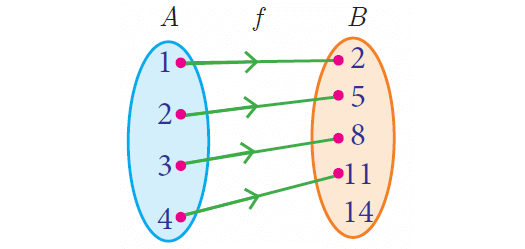
Let A = {1, 2, 3, 4} and B = {2, 5, 8, 11, 14} be two sets.
Let f : A --> B be a function given by f(x) = 3x - 1. Represent this function
(i) by arrow diagram
(ii) in a table form
(iii) as a set of ordered pairs
(iv) in a graphical form
Solution :
A = {1, 2, 3, 4} and B = {2, 5, 8, 11, 14}
f(x) = 3x - 1
f(1) = 3(1) – 1 = 3 – 1 = 2
f(2) = 3(2) – 1 = 6 – 1 = 5
f(3) = 3(3) – 1 = 9 – 1 = 8
f(4) = 4(3) – 1 = 12 – 1 = 11
(i) Arrow diagram :
(ii) Table form :
The given function f can be represented in a tabular form as given below.
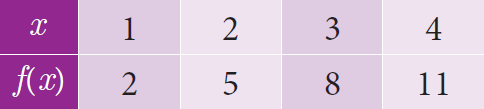
(iii) Set of ordered pairs :
The function f can be represented as a set of ordered pairs as
f = {(1, 2), (2, 5), (3, 8), (4, 11)}
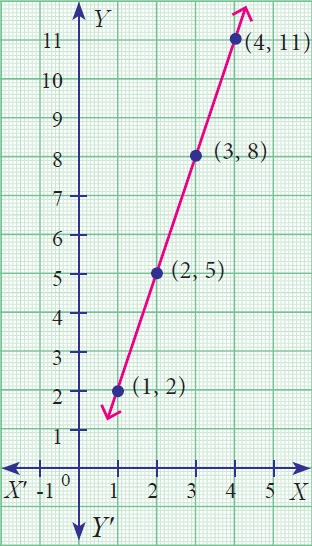
(iv) Graphical form :
We can plot the following points in the xy -plane to get the graphical form.
(1, 2), (2, 5), (3, 8), (4, 11)
Example 2 :
Determine the equations that describe the following function rules:
a) The input is 3 less than the output.
b) The output is 5 less than the input multiplied by 2.
c) Subtract 2 from the input and then multiply by 3 to find the output.
d) The sum of the input and output is 5.
Solution :
Let x be the input and y be the output
a) The input is 3 less than the output.
y = x - 3
b) The output is 5 less than the input multiplied by 2.
y = 2x - 5
c) Subtract 2 from the input and then multiply by 3 to find the output.
y = 3x - 2
d) The sum of the input and output is 5.
x + y = 5
Example 3 :
Martin wants to build an additional closet in a corner of his bedroom. Because the closet will be in a corner, only two new walls need to be built. The total length of the two new walls must be 12 m. Martin wants the length of the closet to be twice as long as the width, as shown in the diagram
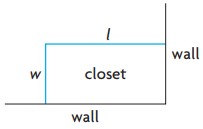
a) Explain why l = 2w
b) Let the function f(l) be the sum of the length and width. Find the equation for f(l).
c) Graph y = f(l)
d) Find the desired the length and width
Solution :
The total length of the two new walls = 12 m
l be the length and w be the width.
l + w = 12
a)
Martin wants the length of the closet to be twice as long as the width. So,
l = 2w
b) From above, w = (1/2)l
Function in terms of l,
f(l) = l + w
Applying the value of w, we get
f(l) = l + (1/2)l
f(l) = (3/2)l
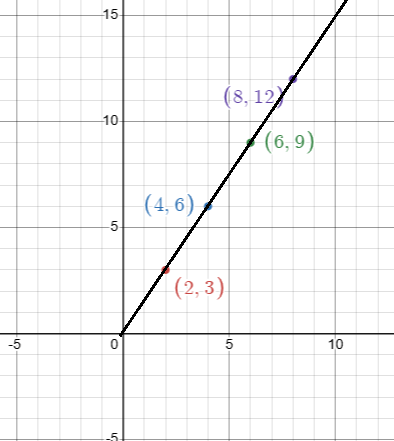
c) y = (3/2)x
|
When x = 2 y = (3/2)2 y = 3 |
When x = 4 y = (3/2)4 y = 6 |
|
When x = 6 y = (3/2)6 y = 9 |
When x = 8 y = (3/2)8 y = 12 |
d) l + w = 12
(3/2)l = 12
l = 12(2/3)
l = 8
w = 12 - 8
w = 4
So, the measures of length and width are 8 m and 4 m resectively.
Example 4 :
The table below lists all the ordered pairs that belong to the function g(x).
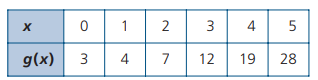
a) Does the equation for g(x).
b) Does g(3) - g(2) = g(3 - 2) explain.
Solution :
a) Let x be the input and y be the output.
y = 2x + 3
b) g(3) = 12 and g(2) = 7
|
L.H.S = g(3) - g(2) = 12 - 7 = 5 |
R.H.S g(3 - 2) = g(1) = 4 |
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
10 Hard SAT Math Questions (Part - 45)
Jan 19, 26 06:14 AM
10 Hard SAT Math Questions (Part - 45) -
10 Hard SAT Math Questions (Part - 44)
Jan 12, 26 06:35 AM
10 Hard SAT Math Questions (Part - 44) -
US Common Core K-12 Curricum Algebra Solving Simple Equations
Jan 07, 26 01:53 PM
US Common Core K-12 Curricum Algebra Solving Simple Equations
