REMAINDER WHEN 2 POWER 256 IS DIVIDED BY 17

In this section, you will learn how to find remainder when 2 power 256 is divided by 17. 

Let us take exponents 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, ....one by one for '2'.

For example, if we take exponent 3 for '2', we get

2³  =  8

Here, 8 is less than the divisor 17 and 8 can not be divided by 17.  

If the dividend is less than the divisor, then the dividend itself has to be considered as 'Remainder'.  

So, when 2³ is divided by 17, the remainder is 8.

If the dividend is greater than the divisor, then we have to divide the dividend by the divisor and get remainder. 

Let us deal our problem in this way. 

When we look at the above table carefully, 2⁰  is divided by 17 and the remainder is 1.

Again we get remainder 1 for power 8.

Next, we will get remainder 1 for power 16. 

So, we get remainder 1, if the exponent of 2 is a multiple of 8.  

In 2²⁵⁶, the exponent is 256.   

This is a multiple of 8. Because

256  =  8 x 32

Because 256 is a multiple of 8, when we divide 2²⁵⁶ by 17, the remainder will be 1. 

What if the exponent is not a multiple of 8? 

Let assume an exponent which is not a multiple of 8.

For example, say the exponent is 263.

What will be the remainder, if 2²⁶³ is divided by 17

The exponent 263 is not a multiple of 8.

Write 263 in terms of multiple of 8 using division algorithm.

263  =  8 x 32 + 7

or

263  =  256 + 7

Then, 

2²⁶³  =  2^{256 + 7}

2²⁶³  =  2²⁵⁶ x 2⁷

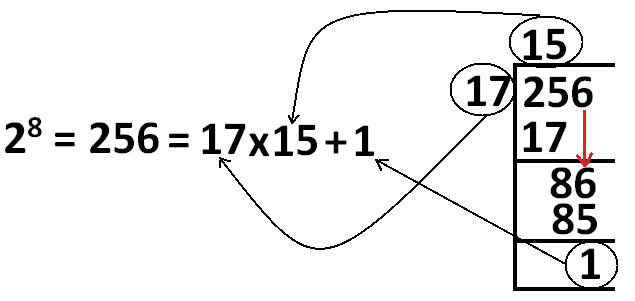
In 2²⁵⁶, the exponent 256 is a multiple of 8.

As explained in the above picture, using division algorithm, we can write 2²⁵⁶ as 

2²⁵⁶  =  17k + 1

Then, 

2²⁶³  =  2²⁵⁶ x 2⁷

2²⁶³  =  (17k + 1) x 2⁷

2²⁶³  =  (17k + 1) x 128

Now we can get the remainder when 2²⁶³ divided by 17 as given below. 

Therefore, the remainder is 9 when 2²⁶³ is divided by 17.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.