RELATIONSHIP BETWEEN SIDES LENGTHS AND ANGLES OF A TRIANGLE

Examples 1-5 : To try to trick you, the following triangles are not drawn to scale. State the largest side of each triangle.

Example 1 :

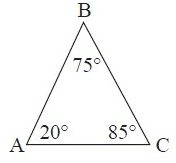
Solution :

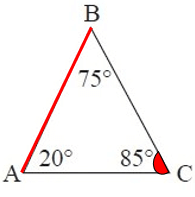
By observing the figure above,

∠C  =  85°,  it is the largest interior angle.

We know that the longest side is always opposite the largest interior angle.

So, the largest side is AB.

Example 2 :

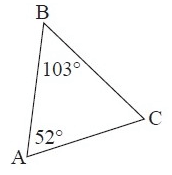
Solution :

By observing the figure, the measure of ∠C is not given. So we have to find ∠C.

We know that, the sum of the interior angles of a triangle is 180˚.

∠A + ∠B + ∠C  =  180°

52° + 103° + ∠C  =  180°

155°+ ∠C  =  180°

Subtract 155° from both sides.

∠C  =  25°

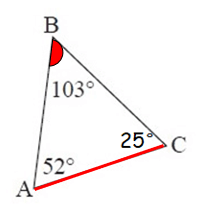
Now, both m∠A and m∠C are less than m<B.

∠B = 103°, it is the largest interior angle.

So, the largest side is AC.

Example 3 :

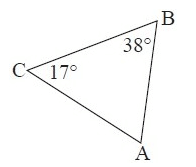
Solution :

By observing the figure, the measure of ∠A is not given.

To find ∠A,

∠A + ∠B + ∠C  =  180°

∠A + 38° + 17°  =  180°

∠A + 55°  =  180°

Subtract 55° from both sides.

∠A  =  125°

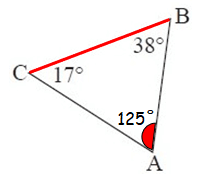
Example 4 :

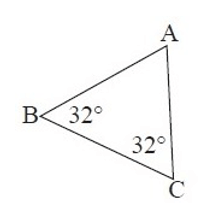
Solution :

By observing the figure, the measure of ∠A is not given.

To find ∠A,

∠A + ∠B + ∠C  =  180°

∠A + 32° + 32°  =  180°

∠A + 64°  =  180°

Subtract 64° from both sides.

∠A  =  116°

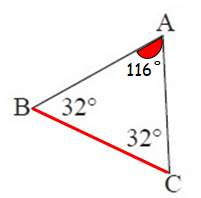
Now, both m∠B and m∠C are less than m∠A.

∠A = 116°, it is the largest interior angle.

So, the largest side is BC.

Example 5 :

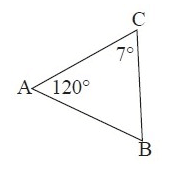
Solution :

By observing the figure, the measure of ∠B is not given.

To find ∠B,

∠A + ∠B + ∠C  =  180°

120˚ + ∠B + 7˚  =  180˚

∠B + 127°  =  180°

Subtract 127° from both sides.

∠B  =  53°

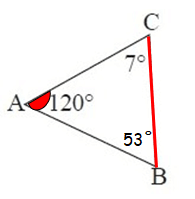
Now, both m∠B and m∠C are less than m∠A.

∠A = 120°, it is the largest interior angle.

So, the largest side is BC.

Example 6 :

The following triangle is not drawn to scale. State the smallest side.

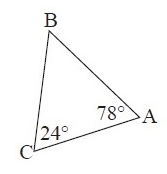
Solution :

By observing the figure, the measure of ∠B is not given.

To find ∠B,

∠A + ∠B + ∠C  =  180°

78° + ∠B + 24°  =  180°

∠B + 102°  =  180°

Subtract 102° from both sides.

∠B  =  78°

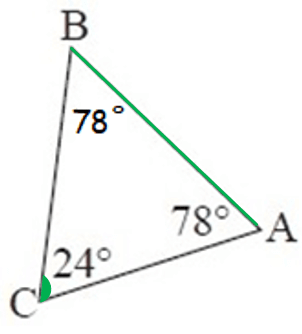
The smallest angle is ∠C, the side which is opposite to smaller angle is AB. So, the smallest side is AB.

To try to trick you, the following triangles are not drawn to scale. State the largest side of each triangle.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.