RELATED RATES WORD PROBLEMS AND SOLUTIONS
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
The derivative can be used to
determine the rate of change of one variable with respect to another. A few examples are population
growth rates, production rates, water flow rates, velocity, and acceleration.
Rates of change with respect to some other quantity in our daily life are given below :
1) Slope is the rate of change in vertical length with respect to horizontal length.
2) Velocity is the rate of displacement with respect to time.
3) Acceleration is the rate of change in velocity with respect to time.
4) The steepness of a hillside is the rate of change in its elevation with respect to linear distance
The average rate of change in an interval [a, b] is
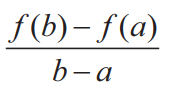
whereas, the instantaneous rate
of change at a point x is f′(x) for the given function.
Example 1 :
A particles moves along a line according to the law
s(t) = 2t3 – 9t2 +12t
– 4, where t > 0.
(i) At what time the particle changes direction?
(ii) Find the total distance travelled by the particle in the first 4 seconds.
(iii) Find the particle’s acceleration each time the velocity is zero.
Solution :
(i) The particle changes direction when velocity changes its sign.
Now, v(t) = = 6t2 – 18t + 12 = 0 gives t = 1 and t = 2.
If 0 ≤ t < 1 then both (t - 1) and (6t - 12) < 0, then
v(t) > 0
If 1 < t < 2 then both (t - 1) 0 and (6t - 12) 0, then
So, v(t) < 0
If t > 2 then both (t - 1) and (6t - 12) > 0, then
v(t) > 0
So, the particle changes direction when t = 1 and t = 2.
(ii) Given s(t) = 2t3 – 9t2 +12t – 4 ----(1),
From (1),
s(0) = 2(0)3 - 9(0)2 + 12(0) – 4 = -4
s(1) = 2(1)3 - 9(1)2 + 12(1) – 4 = 1
s(2) = 2(2)3 - 9(2)2 + 12(2) – 4 = 0
s(3) = 2(3)3 - 9(3)2 + 12(3) – 4 = 5
s(4) = 2(4)3 - 9(4)2 + 12(4) – 4 = 28
The total distance traveled by the particle in the first 4 seconds,
|s(1) - s(0)| + |s(2) - s(1)| + |s(3) - s(2)| + |s(4) - s(3)|
= |1 - (-4)| + |0 - 1| + |5 - 0| + |28 - 5|
= 34
So, the total distance traveled by the particle in the first 4 seconds is 34 m
(iii)The acceleration is given by a(t) = 12t – 18.
Velocity is zero, when t = 1 and t = 2.
Therefore, the acceleration when t = 1 sec is -6 m/sec2 and the acceleration when t = 2 sec is 6 m/sec2.
Example 2 :
If the volume of a cube of side length x is v = x3. Find the rate of change of the volume with respect to x when x = 5 units.
Solution :
The rate of change of the volume with respect to length x is 3x2.
The rate of change of the volume with respect to x, when x = 5 units is
= 3(5)2
= 75 units
Example 3 :
If the mass m(x) (in kilogram) of a thin rod of length x (in meters) is given by, m(x) = √(3x) then what is the rate of change of mass with respect to the length when it is x=3 and x = 27 meters.
Solution :
The rate of change of mass with respect to the length is
dm/dx = √3/√(2x)
When x = 3, dm/dx = (1/2) kg/m.
When x = 27, dm/dx = (1/6) kg/m.
Example 4 :
A stone is dropped into a pond causing ripples in the form of concentric circles. The radius r of the outer ripple is increasing at a constant rate at 2 cm per second. When the radius is 5 cm find the rate of changing of the total area of the disturbed water?
Solution :
Given : The radius r of the outer ripple is increasing at a constant rate at 2 cm/sec.
Total area of a circle is a = π r2
The rate of change of the total area = 2πr((dr/dt)
The rate of changing of the total area when the radius is 5 cm.
= 2π(5)(2)
= 20π
So, the rate of changing of the total area of the disturbed water when the radius is 5 cm is 20π sq.cm/sec.
Example 5 :
An airplane is flying towards a radar station at a constant height of 6 km above the ground. If the distance between the airplane and the radar station is decreasing at the rate of 400 km per hour when s = 10 km, what is the horizontal speed of the plane ?
Solution :
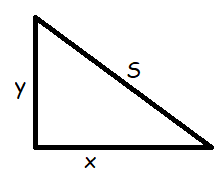
x2 + y2 = S2
y = 6, S = 10, x = ?
102 = x2 + 62
100 - 36 = x2
x2 = 64
x = 8
ds/dt = -400 km/h
Differentiating with respect to t, we get
2x (dx/dt) + 0 = 2S (ds/dt)
2(8) (dx/dt) = 2(10) (-400)
dx/dt = -8000/16
= -500
So, the horizontal speed of the plane is toward the station is 500 km per hour.
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
10 Hard SAT Math Questions (Part - 44)
Jan 12, 26 06:35 AM
10 Hard SAT Math Questions (Part - 44) -
US Common Core K-12 Curricum Algebra Solving Simple Equations
Jan 07, 26 01:53 PM
US Common Core K-12 Curricum Algebra Solving Simple Equations -
10 Hard SAT Math Questions (Part - 4)
Jan 05, 26 06:56 PM
10 Hard SAT Math Questions (Part - 4)
