REGRESSION ANALYSIS

In regression analysis, we are concerned with the estimation of one variable for a given value of another variable (or for a given set of values of a number of variables) on the basis of an average mathematical relationship between the two variables (or a number of variables).

Regression analysis plays a very important role in the field of every human activity.

A businessman may be keen to know what would be his estimated profit for a given level of investment on the basis of the past records.

Similarly, an outgoing student may like to know her chance of getting a first class in the final University Examination on the basis of her performance in the college selection test.

Regression Analysis

When there are two variables x and y and if y is influenced by x i.e. if y depends on x, then we get a simple linear regression or simple regression.

y is known as dependent variable or regression or explained variable and x is known as independent variable or predictor or explanator.

In the previous examples since profit depends on investment or performance in the University Examination is dependent on the performance in the college selection test, profit or performance in the University Examination is the dependent variable and investment or performance in the selection test is the In-dependent variable.

In case of a simple regression model if y depends on x, then the regression line of y on x in given by

y = a + bx

Here a and b are two constants and they are also known as regression parameters.

Furthermore, b is also known as the regression coefficient of y on x and is also denoted by bᵧₓ and the formula to find bᵧₓ is given by

Here, r stands for correlation coefficient between x and y.

After estimating b, estimate of a_yx is given by

If x depends on y, then the regression line of x on y in given by

x = a + by

Here a and b are two constants and they are also known as regression parameters.

Furthermore, b is also known as the regression coefficient of x on y and is also denoted by bₓᵧ.

Here, r stands for correlation coefficient between x and y.

After estimating b, estimate of a_xy is given by

Problem :

Find the two regression equations from the following data :

x  :     2     4     5      5      8      10

y  :     6     7     9     10     12     12

Solution :

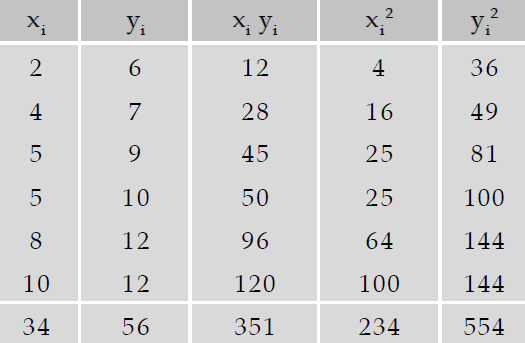
On the basis of the above table, we have

The regression line of y on x is given by

y = a + bx

where

Thus the estimated regression equation of y on x is

y = 4.7178 + 0.8145x

Similarly, the regression equation of x on y can be calculated and it is  

x = –4.3601 + 1.0743y

Properties of Regression Lines

(i) The regression coefficients remain unchanged due to a shift of origin but change due to a shift of scale.

This property states that if the original pair of variables is (x, y) and if they are changed to the pair (u, v) where

(ii) The two lines of regression intersect at the point

where x and y are the variables under consideration. 

(iii) The coefficient of correlation between two variables x and y in the simple geometric mean of the two regression coefficients. The sign of the correlation coefficient would be the common sign of the two regression coefficients.

This property says that if the two regression coefficients are denoted by b_yx and b_xy then the coefficient of correlation is given by

If both the regression coefficients are negative, r would be negative and if both are positive, r would assume a positive value.

(iv) The two lines of regression coincide i.e. become identical when r = –1 or 1 or in other words, there is a perfect negative or positive correlation between the two variables under discussion.

(v) The two lines of regression are perpendicular to each other when r = 0. 

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.