REFLEXIVE PROPERTY OF CONGRUENCE

When two shapes or figures have the same shape and size, we use the term congruence and they shapes or figures are said to be congruent (≅).

In geometry, the reflexive property of congruence  states that an angle, line segment, or shape is always congruent to itself.

Every triangle is congruent to itself. 

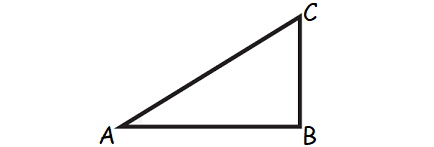
In the diagram above, triangle ABC is congruent to it self.

Example 1 :

Prove every triangle is congruent to itself.

Solution :

If two triangle are considered to be congruent, they have to meet the following two conditions.

1. They must have exactly the same three sides.

2. They must have exactly the same three angles.

Every triangle and itself will meet the above two conditions. 

So, every triangle is congruent to itself.

Example 2 :

In the picture shown below, prove ΔABC and ΔDBA are similar. 

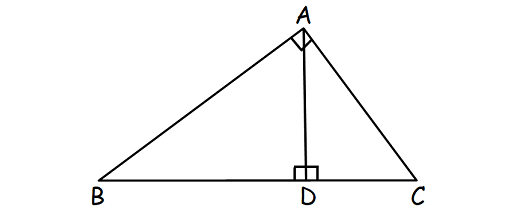
Solution :

In right triangles ABC and DBA above,

∠BAC ≅ ∠ADC (Right Angles)

By Reflexive Property of Congruence,

∠ABC ≅ ∠ABD

(an angle is congruent to itself)

Two angles of ΔABC are congruent to ΔDBA.

By Angle-Angle Similarity Postulate,

ΔABC ∼ ΔDBA

Example 3 :

In the picture shown below, prove ΔWXY and ΔZWY are similar. 

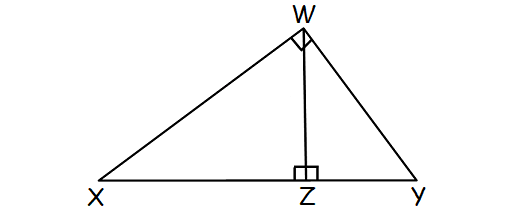
Solution :

In right triangles WXY and DBA above,

∠XWY ≅ ∠WZY (Right Angles)

By Reflexive Property of Congruence,

∠WYX ≅ ∠WYZ

(an angle is congruent to itself)

Two angles of ΔWXY are congruent to ΔZWY.

By Angle-Angle Similarity Postulate,

ΔWXY ∼ ΔZWY

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.