REFLECTION TRANSFORMATION MATRIX

Reflection transformation matrix is the matrix which can be used to make reflection transformation of a figure.

We can use the following matrices to get different types of reflections.

Reflection about the x-axis

Reflection about the y-axis

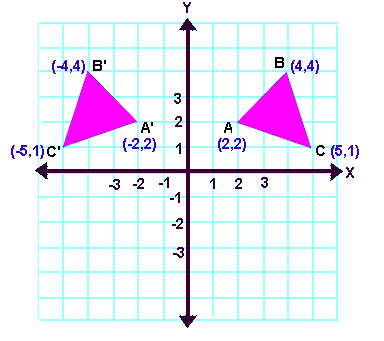
Reflection about the line y = x

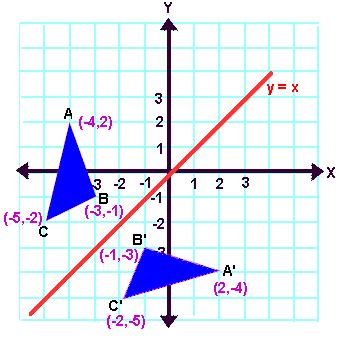
Once students understand the rules which they have to apply for reflection transformation, they can easily make reflection  transformation of a figure.

Let us consider the following example to have better understanding of reflection.

Question :

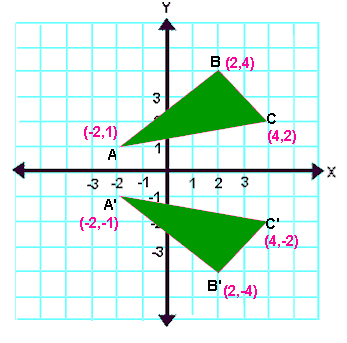
Let A ( -2, 1), B (2, 4) and (4, 2) be the three vertices of a triangle. If this triangle is reflected about x-axis, find the vertices of the reflected image A'B'C' using matrices.

Solution :

Step 1 :

First we have to write the vertices of the given triangle ABC  in matrix form as given below.

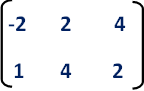
Step 2 :

Since the triangle ABC is reflected about x-axis, to get the reflected image, we have to multiply the above matrix by  the matrix given below.

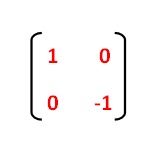
Step 3 :

Now, let us multiply the two matrices.

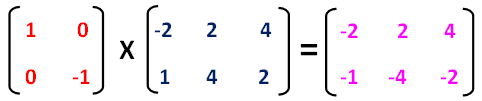
Step 4 :

Now we  can get vertices of the reflected image A'B'C' from the resultant matrix.

Vertices of the reflected image are

A'(-2, -1), B'(2, -4) and C'(4, -2)

After having gone through the example given above, we hope that the students would have understood the way in which they have to find the vertices of the reflected image using matrices.

Reflecting over Any Line

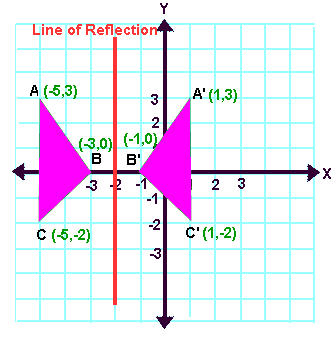
When we look at the above figure, it is very clear that each point of a reflected image A'B'C' is at the same distance from the line of reflection as the corresponding point of the original figure.

In other words, the line x = -2 (line of reflection) lies directly in the middle between the original figure and its image.

And also, the line x = -2 (line of reflection) is the perpendicular bisector of the segment joining any point to its image.

Students can keep this idea in mind when they are working with lines of reflections which are neither the x-axis nor the y-axis.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.