REDUCING EACH RATIONAL EXPRESSIONS TO LOWEST TERMS

Example 1 :

Express in simplest form.

x/(x²)

Solution :

=  x/(x²)

=  1/x

So, the answer is 1/x.

Example 2 :

Express in simplest form.

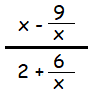
Solution :

By using cross multiplication, we get

= (x² - 9)/x / (2x + 6)/x

= (x² - 9)/x ⋅ x/(2x + 6)

= (x² - 9)/2(x + 3)

Using algebraic identity a² - b², we get

a² - b² = (a + b)(a - b)

= (x + 3) (x - 3)/2(x + 3)

= (x - 3) / 2

So, the answer is (x - 3)/2.

Example 3 :

Express in simplest form.

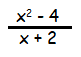
Solution :

x² - 4 = x² - 2² = (x + 2)(x - 2)

Applying factored form in the numerator, we get

= (x + 2)(x - 2) / (x + 2)

= x - 2

So, the answer is x - 2.

Example 4 :

Express in simplest form.

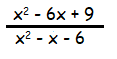
Solution :

Factoring the numerator :

= x² - 6x + 9

= x² - 3x - 3x + 9

= x(x - 3) - 3(x - 3)

= (x - 3)(x - 3)

Factoring the denominator :

= x² - x - 6

= x² - 3x + 2x - 6

= x(x - 3) + 2(x - 3)

= (x + 2)(x - 3)

Writing the factored form in the numerator and denominator :

= (x - 3)(x - 3) / (x + 2)(x - 3)

= (x - 3) / (x + 2)

Example 5 :

Express in simplest form.

The expression (x²y² - 9)/(3 - xy) is equivalent to 

(A)  -1     (B)  1/(3 + xy)     (C)  -(3 + xy)     (D)  3 + xy

Solution :

(x²y² - 9)/(3 - xy)

Factoring the numerator :

 x²y² - 9 = (xy)² - 3²

= (xy - 3)(xy + 3)

The denominator :

= (3 - xy)

= -(xy - 3)

Writing the factored form, we get

= (xy - 3)(xy + 3) / -(xy - 3)

= -(xy + 3)

So, the answer is -(xy + 3)

Example 6 :

Express in simplest form.

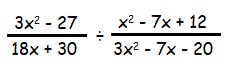
Solution :

= 3x² - 27

Factoring 3, we get

= 3(x² - 9)

= 3(x² - 3²)

= 3(x + 3)(x - 3)  ----(1)

= 18x + 30

Factoring 6, we get

= 6(3x + 5) ----(2)

x² - 7x + 12 = x² - 4x - 3x + 12

= x(x - 4) - 3(x - 4)

= (x - 4)(x - 3)  ----(3)

3x² - 7x - 20 = 3x² - 12x + 5x - 20

= 3x(x - 4) + 5(x - 4)

= (x - 4)(3x + 5)  ----(4)

(1) / (2) ÷ (3) / (4)

= [3(x + 3)(x - 3) / 6(3x + 5)] ÷ [ (x - 4)(x - 3) / (x - 4)(3x + 5)]

= [3(x + 3)(x - 3) / 6(3x + 5)] ⋅ [ (x - 4)(3x + 5)/(x - 4)(x - 3)]

= (x + 3) / 2

So, the answer is (x + 3)/2.

Example 7 :

Expressed as a fraction in lowest terms, 

(x² - x - 2)/(x² - 4), x ≠ ±2 is equivalent to

(A)  x/(x+2)    (B)  (x-1)/(x-2)   (C)  (x+1)/(x+2)   

(D) (-x-2)/(-4)

Solution :

= (x² - x - 2)/(x² - 4)

Factoring the numerator :

x² - x - 2 = x² - 2x + 1x - 2

= x(x - 2) + 1(x - 2)

= (x + 1)(x - 2) -------(1)

x² - 4 = x² - 2²

= (x - 2)(x + 2)  -------(2)

(1) / (2)

= (x + 1)(x - 2) / (x - 2)(x + 2)

= (x + 1) / (x + 2)

So, the answer is (x + 1)/(x + 2).

Example 8 :

What is (6x² - 4x)/(2x² - 4x) reduced to simplest term ?

(A)  (3x-2)/(x+2)    (B)  (3x+2)/(x-2)   (C)  (3x+2)/(x+2)   

(D) (3x-2)/(x-2)

Solution :

By taking common factor, we get

6x² - 4x = 2x(3x - 2)

2x² - 4x = 2x(x - 2)

= 2x(3x - 2) / 2x(x - 2)

= (3x - 2) / (x - 2)

So, the answer is (3x - 2)/(x - 2).

Example 9 :

What is (x² + x - 20)/(4 - x) expressed in simplest form ?

(A)  -x - 5    (B)  x + 5  (C)  5 - x   (D)  x - 5

Solution :

= (x² + x - 20)/(4 - x)

x² + x - 20 = x² + 5x - 4x - 20

= x(x + 5) - 4(x + 5)

= (x - 4)(x + 5)

from 4 - x, factoring negative we get

= -(x - 4)

= (x - 4)(x + 5) / -(x - 4)

= -(x + 5)

So, the answer is -x - 5.

Example 10 :

Expressed in simplest form, 

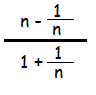
is equivalent to

(A)  n + 1    (B)  n  (C)  n - 1   (D)  (n - 1)/(n + 1)

Solution :

By cross multiplication, we get

= [(n² - 1) / n] / [(n + 1) / n]

= [(n + 1)(n - 1)) / n] x [n / (n + 1)]

= (n - 1)

So, the answer is n - 1.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.