RECURSIVE DEFINITION FOR ARITHMETIC SEQUENCES

An arithmetic sequence is a sequence in which the difference between any two consecutive terms is constant along the sequence.

Understanding Arithmetic Sequences

Example 1 :

Is the sequence arithmetic ? If so, what is the common difference ? What is the next term in the sequence ?

3, 8, 13, 18, 23,.............

Solution :

This is a sequence, a function whose domain is the Natural numbers. 

Create a table that shows the term number, or domain, and the term, or range.   

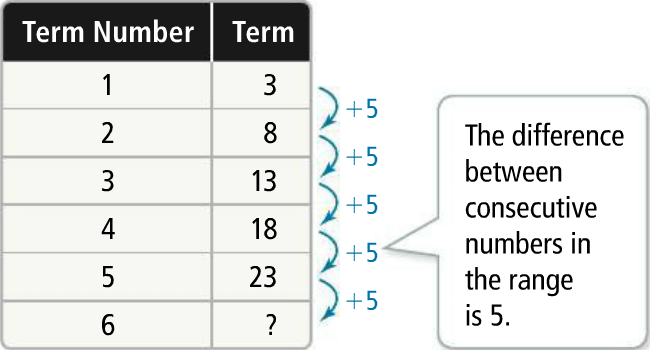
An arithmetic sequence is a sequence with a constant difference between consecutive terms. The difference is known as the common difference, or d.  

This sequence is an arithmetic sequence with common difference,

d  =  5 

The next term in the sequence is

23 + 5, or 28

Recursive Definition for Arithmetic Sequences

In an arithmetic sequence, each term can be represented by f(n) where n represents the number of a particular term. 

Let us consider an arithmetic sequence where the first term is 3 and the common difference is 5. 

So, for n  =  1,

f(1)  =  3

If n > 1, each term is the sum of the previous term and the common difference 5.

f(2)  =  f(1) + 5

f(3)  =  f(2) + 5

f(4)  =  f(3) + 5

In this way, we have

f(n)  =  f(n - 1) + 5

Write the general rule for an arithmetic sequence as a piecewise-defined function :

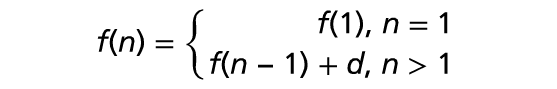
This is the recursive definition for an arithmetic sequence. Each term is defined by operations on the previous term.

Another way to write recursive definition for an arithmetic sequence is  

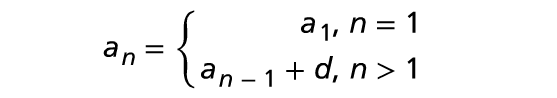
In the notation shown above, the subscript shows the number of the term.

Example 2 :

Is the sequence 7, 10, 13, 16, ........... arithmetic ? If so, write the recursive definition for the sequence. 

Solution :

In the given sequence, difference between any two consecutive terms along the sequence is 3. 

So, this is an arithmetic sequence. 

The recursive definition for this sequence is 

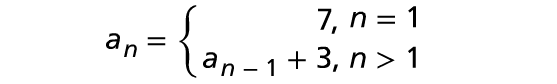
Difference Between Recursive and Explicit

The main difference between recursive and explicit is that a recursive formula gives the value of a specific term based on the previous term while an explicit formula gives the value of a specific term based on the position.

In general, the explicit definition of an arithmetic sequence is

a_n  =  a₁ + d(n - 1)

Translation Between Recursive and Explicit Forms

Example 3 :

Given the recursive definition : 

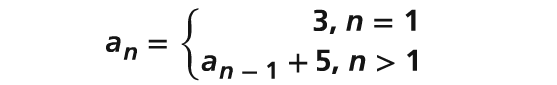
What is an explicit definition for the sequence ?

Solution :

An explicit definition, also written as 

a_n  =  a₁ + d(n - 1)

allows us to find any term in the sequence without knowing the previous term. 

Use the recursive definition to find a pattern : 

a₁  =  3  =  3 + 0(5)

a₂  =  a₁ + 5  =  3 + 5  =  3 + 1(5)

a₃  =  a₂ + 5  =  8 + 5  =  [3 + 5] + 5  =  3  + 2(5)

a₄  =  a₃ + 5  =  13 + 5  =  [3 + 5 + 5] + 5  =  3 + 3(5)

So, the explicit form is 

a_n  =  3 + (n - 1)(5)

Example 4 :

Given the explicit definition : 

a_n  =  16 + 3(n - 1)

What is the recursive definition for the arithmetic sequence ?

Solution :

Comparing a_n  =  a₁ + d(n - 1) and a_n  =  16 + 3(n - 1), we get  

the common difference d  =  3 and a₁  =  16

Hence, the recursive definition is

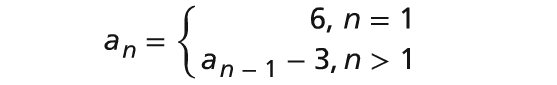
Example 5 :

A high school auditorium has 20 seats in the first row and 35 seats in the sixth row. The number of seats in each row forms an arithmetic sequence. 

A. What is the explicit definition for the sequence ?

B. How many seats are in the thirteenth row ? 

Solution (A) :

The problem states that 

a₁  =  20, n  =  6 and a₆  =  35

Write the general explicit formula. 

a_n  =  a₁ + d(n - 1)

Substitute.

35  =  20 + d(6 - 1)

Simplify.

35  =  20 + 5d

Subtract 20 from each side. 

15  =  5d

Divide each side by 5.

3  =  d

So, each row has two more seats than the previous row. 

Then, the explicit definition is

a_n  =  20 + 3(n - 1)

Solution (B) :

Write the explicit formula. 

a_n  =  20 + 3(n - 1)

We have to find the number of seats in thirteenth row. So we have substitute 13 for n.

a₁₃  =  20 + 3(13 - 1)

Simplify.

a₁₃  =  20 + 3(12)

a₁₃  =  20 + 36

a₁₃  =  56

Hence, there are 56 seats in thirteenth row. 

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.