RECIPROCAL IN MATHEMATICS
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Reciprocal of a number is nothing but its multiplicative inverse.
Let us consider the fraction 3/4.
If we want to get its reciprocal, we have write the denominator 4 as numerator and numerator 3 as denominator.
In simple words, we have to flip the fraction.
So, the reciprocal of 3/4 is 4/3. And also the reciprocal of 4/3 is 3/4.
Therefore, 3/4 and 4/3 are reciprocal to each other.
Important note :
If two numbers are reciprocal to each other, then their product is 1.
That is,
(3/4) x (4/3) = 1
Reciprocal of a Whole Number
Let us consider the whole number 8.
If we want to get reciprocal of the whole number 8, first we have write 8 as a fraction with denominator 1.
That is 8/1.
To get reciprocal of 8/1, we have write the denominator 1 as numerator and numerator 8 as denominator.
That is 1/8.
Therefore, the reciprocal of the whole number 8 is 1/8.
And also,
8 x 1/8 = 1
It has been illustrated in the diagram given below.
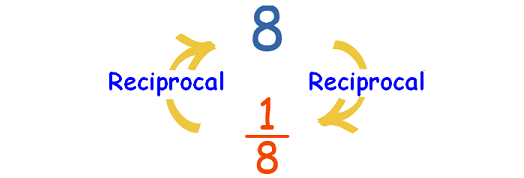
Shortcut :
If we want to get reciprocal of any whole number, we have to write 1 as numerator and the given whole number as denominator.
Reciprocal of 1
The reciprocal of 1 is 1 itself.
Let us see, how the reciprocal of 1 is 1 itself.
To get the reciprocal of 1, let us write 1 as a fraction with denominator 1.
That is 1/1.
To get reciprocal of 1/1, we have write the denominator 1 as numerator and numerator 1 as denominator.
That is 1/1.
Therefore, the reciprocal of the whole number 1 is 1 itself.
Reciprocal of Zero
The reciprocal of zero is undefined.
Let us see, how the reciprocal of zero is undefined.
To get the reciprocal of 0, let us write 0 as a fraction with denominator 1.
That is 0/1.
To get reciprocal of 0/1, we have to write the denominator 1 as numerator and numerator 0 as denominator.
Then, we have 1/0.
Here, 1 is divided by 0.
In Math, any non zero number divided by zero is undefined.
Therefore, the reciprocal of zero is undefined.
Reciprocal of ∞
The reciprocal of ∞ is zero.
Let us see, how the reciprocal of infinity is zero.
In Math infinity (∞) is the symbol that we use for the term "Undefined".
To get the reciprocal of ∞, let us write ∞ as a fraction 1/0.
Because, any non zero number divided by zero is undefined or infinity.
To get reciprocal of 1/0, we have write the denominator 0 as numerator and numerator 1 as denominator.
Then, we have 0/1.
Here, 0 is divided by 1.
In Math, zero divided by any non zero number is zero.
Therefore, the reciprocal of infinity (∞) is zero.
Reciprocal of Mixed Number
Let us consider the mixed number 2 3/4.
To get the reciprocal of 2 3/4, let us convert the given mixed number 2 3/4 into improper fraction.
Then, we have
2 3/4 = 11/4
To get reciprocal of 11/4, we have to write the denominator 4 as numerator and numerator 11 as denominator.
Then, we have 4/11.
Therefore, the reciprocal of 2 3/4 is 4/11.
Using Reciprocal to Divide Fractions
Step 1 :
When we divide a fraction by another fraction, first we have to change the division sign as multiplication.
Step 2 :
Take reciprocal of the second fraction.
Step 3 :
Multiply the two fractions. (Numerator times numerator and denominator times denominator).
Example 1 :
Divide 2/5 by 6/7.
Solution :
Using the method explained above, we have
2/5 ÷ 6/7 = 2/5 x 7/6
2/5 ÷ 6/7 = (2x7) / (5x6)
2/5 ÷ 6/7 = 7/15
Example 2 :
Divide 7/5 by 3/2.
Solution :
ained above, we have
7/5 ÷ 3/2 = 7/5 x 2/3
7/5 ÷ 3/2 = (7x2) / (5x3)
7/5 ÷ 3/2 = 14/15
Example 3 :
Divide 5/12 by 20/13.
Solution :
Using the method explained above, we have
5/12 ÷ 20/13 = 5/12 ÷ 20/13
5/12 ÷ 20/13 = 5/12 x 13/20
5/12 ÷ 20/13 = (5x13) / (12x20)
5/12 ÷ 20/13 = 13/48
Example 4 :
Divide 2/19 by 6 1/2.
Solution :
First, let us convert the mixed number 6 1/2 in to improper fraction.
6 1/2 = 13/2
Now,m we have 2/19 ÷ 6 1/2 = 2/19 ÷ 13/2
Using the method explained above, we have
2/19 ÷ 13/2 = 2/19 x 13//2
2/19 ÷ 13/2 = (2x13) / (19x2)
2/19 ÷ 13/2 = 13 / 19
Example 5 :
One pizza can be made in 1/2 hour. How many pizzas can be made in 5/2 hours ?
Solution :
Time taken to make one pizza = 1/2 hour
No. of pizzas made in 5/2 hours = 5/2 ÷ 1/2
No. of pizzas made in 5/2 hours = 5/2 x 2/1
No. of pizzas made in 5/2 hours = (5x2) / (2x1)
No. of pizzas made in 5/2 hours = 5
Using Fractions to Divide Fractions by Whole Numbers
Step 1 :
When we divide a fraction by a whole number, first we have to write the whole number as fraction with denominator 1.
Step 2 :
Change the division sign as multiplication.
Step 3 :
Take reciprocal of the second fraction (Whole number with denominator 1).
Step 4 :
Multiply the two fractions. (Numerator times numerator and denominator times denominator).
Example 1 :
Simplify : 2/5 ÷ 6
Solution :
Using method 1, we have
2/5 ÷ 6 = 2/5 ÷ 6/1
2/5 ÷ 6 = 2/5 x 1/6
2/5 ÷ 6 = (2x1) / (5x6)
2/5 ÷ 6 = 1/15
Example 2 :
Simplify : 5/12 ÷ 20
Solution :
Using method 2, we have
5/12 ÷ 20 = 5 / (12x20)
5/12 ÷ 20 = 1/48
Example 3 :
David eats 1/4 of a pizza and divides the remaining in to two equal parts for his two kids. What is the part of the pizza will each kid receive ?
Solution :
Part of the pizza eaten by David = 1/4
Remaining pizza = 3/4
Given : Remaining pizza is divided in to equal parts for his two kids.
So, part of the pizza received by each kid is
= 3/4 ÷ 2
= 3/(4x2)
= 3/8
Hence, each kid will receive 3/8 part of the pizza.
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
10 Hard SAT Math Questions (Part - 44)
Jan 12, 26 06:35 AM
10 Hard SAT Math Questions (Part - 44) -
US Common Core K-12 Curricum Algebra Solving Simple Equations
Jan 07, 26 01:53 PM
US Common Core K-12 Curricum Algebra Solving Simple Equations -
10 Hard SAT Math Questions (Part - 4)
Jan 05, 26 06:56 PM
10 Hard SAT Math Questions (Part - 4)
