REAL WORLD PROBLEMS INVOLVING AREA AND PERIMETER

Problem 1 :

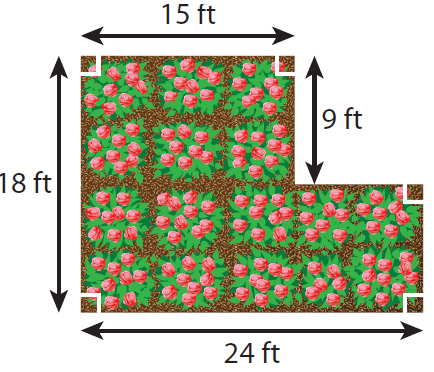
The diagram shows the shape and dimensions of Teresa’s rose garden.

(a) Find the area of the garden.

(b) Teresa wants to buy mulch for her garden. One bag of mulch covers 12 square feet. How many bags will she need?

Solution :

By drawing a horizontal line, we can divide the given shape into two parts as shown below.

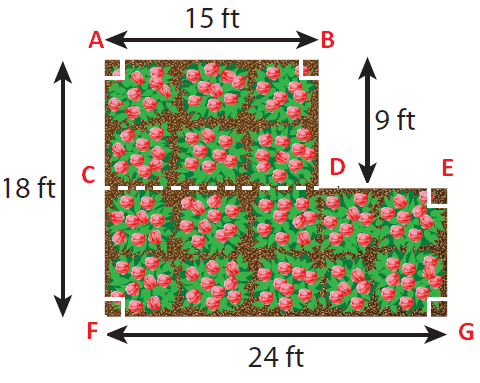
(1) ABCD is a rectangle

(2) CEFG is also a rectangle

Area of the garden

= Area of rectangle ABCD + Area of the rectangle CEFG

Area of rectangle ABCD :

length AB = 15 ft and width BD = 9 ft

= length x width 

 =  15 x 9

=  135 ft²  ----(1)

Area of rectangle CEFG :

length CE = 24 ft and width CF = AF - AC ==> 18 - 9 = 9 ft

= length x width 

 =  24 x 9

=  216 ft²  ----(1)

(1) + (2) 

Area of the rose garden = 135 + 216 ==> 351 ft²

Number of bags that she needed = 351/12 ==> 29.25

So, she will need 30 bags of mulch

Problem 2 :

The length of a rectangle is 4 less than 3 times its width. If its length is 11 cm, then find the perimeter. 

Solution :

Let w be the width of the rectangle.

Then, its length is (3w - 4).

Given : Length is 11 cm. 

Then, 

Length (l)  =  11

3w - 4  =  11

3w  =  15

w  =  5

So, the perimeter of the rectangle is 

=  2(l + w)

=  2(11 + 5)

=  2(16)

=  32 cm

Problem 3 :

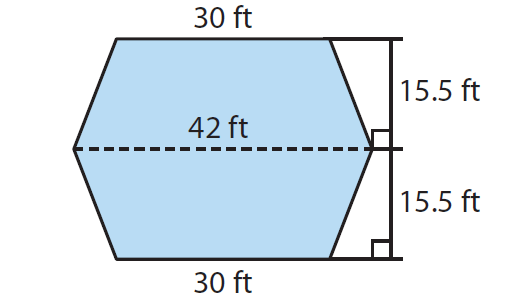
The diagram shows the floor plan of a hotel lobby. Carpet costs $3 per square foot. How much will it cost to carpet the lobby?

Solution :

By observing the above picture, we can find two trapeziums of same size. Since both are having same size. We can find area of one trapezium and multiply the area by 2.

Area of trapezium = (1/2) h (a +  b)

h = 15.5 ft  a = 30 ft  and b = 42 ft

  =  (1/2) x 15.5 x (30 + 42)

  =  (1/2) x 15.5 x 72 ==> 15.5 x 36==> 558 square feet

Area of floor of a hotel lobby = 2 x 558

 =  1116 square feet

Cost of carper per square feet = $3

=  3 x 1116 ==> $ 3348

Amount spent for carpet =  $ 3348.

Problem 4 :

The cost of fencing a circle shaped garden is $20 per foot. If the radius of the garden is 14 feet, find the total cost of fencing the garden. (π  =  22/7). 

Solution :

To know the length of fencing required, find the circumference of the circle shaped garden.

Circumference of the circle shaped garden is 

=  2πr

Substitute 22/7 for π and 14 for r. 

=  2(22/7)(14)

=  88 feet

Total cost of fencing is 

=  88(20)

=  $1760

Problem 5 :

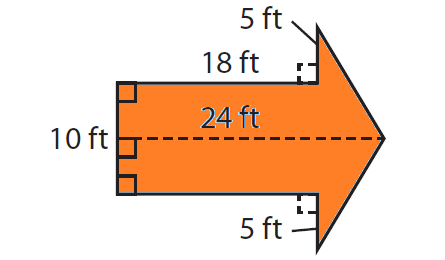
Jess is painting a giant arrow on a playground. Find the area of the giant arrow. If one can of paint covers 100 square feet, how many cans should Jess buy?

Solution :

Now we are going to divide this into three shapes. Two triangles and one rectangle.

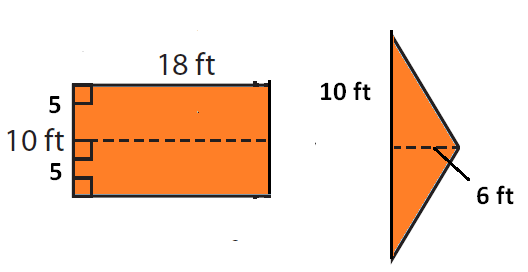
Area of rectangle = length x width

   =  18 x 10 ==> 180 square feet

Area of one triangle = (1/2) x b x h

   =  (1/2) x 6 x 10 ==> 30 square feet

Area of two triangles = 2 x 30 = 60 square feet

Total area of the given shape = 180 + 60

=  240 square feet

one can of paint covers 100 square feet

Number of cans needed = 240/100 = 2.4 approximately 3.

So, Jessy has to 3 cans of paint.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.