RATIOS RATES TABLES AND GRAPHS

In this section, you will learn how to determine the ratio or rate of change of a relation from a table or graph. Students will also compare and contrast ratios, rates, and rates of change.

Example 1 :

Students in Mr. Webster’s science classes are doing an experiment that requires 250 milliliters of distilled water for every 5 milliliters of ammonia. The table shows the amount of distilled water needed for various amounts of ammonia.

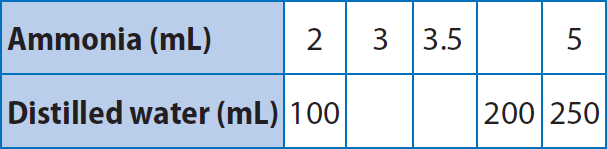
Question (i) : 

Use the numbers in the first column of the table to write a ratio of distilled water to ammonia.

Answer :

100 ml distilled water/2 ml ammonia  (or)  100 : 2

Question (ii) : 

How much distilled water is used for 1 milliliter of ammonia?

Answer :

From the first column of the table, the ratio  of distilled water to ammonia is 

100 ml water/2 ml ammonia

To find the quantity of distilled water used for 1 milliliter of ammonia, we have to make the second quantity (ammonia) as 1. 

100 ml distilled water : 2 ml ammonia = (100 ÷ 2)/(2 ÷ 2)

100 ml distilled water : 2 ml ammonia = 50/1

That is,

50 ml distilled water / 1 ml ammonia  

The quantity of distilled water used for 1 milliliter of ammonia is 50 ml.

Question (iii) : 

Use your answer from question 2, write another ratio of distilled water to ammonia.

Answer :

To write another ratio from the answer of question 2, we have find an equivalent ratio to 50 : 1.

To find equivalent ratio of the given ratio, we have to multiply both the terms of the ratio by the same non zero number, say "2".

Then, we have 

(50 x 2) : (1 x 2) = 100 : 2

Therefore, another ratio of distilled water to ammonia is 100 : 2

Question (iv) : 

Check whether the two ratios from answers of question 1 and question 2 are equivalent or not equivalent. 

Answer :

The two ratios from the answers of question 1 and 2 are 

100 : 2 and 50 : 1 

Let us check, whether two rations 100 : 2 and 50 : 1 are equivalent or not equivalent.

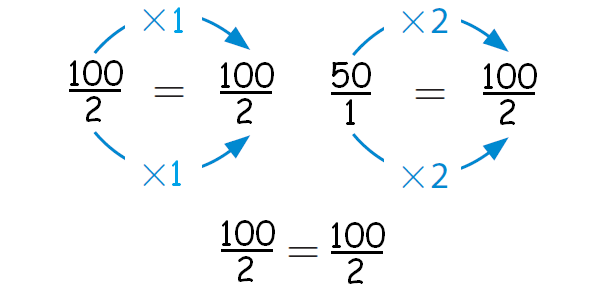
From the above working, it is clear that the two ratios 100 : 2 and 50 : 1 are equivalent.

Question (v) :

Complete the table. What are the equivalent ratios shown in the table?

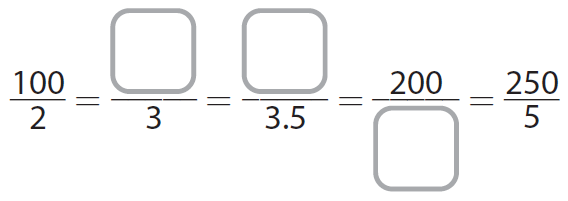
Answer :

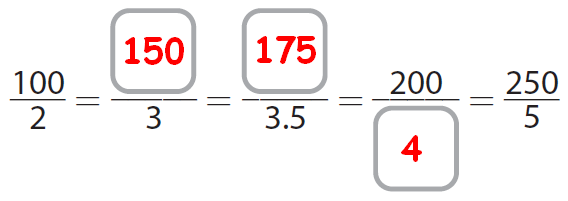
For the first blank :

(100 ÷ 2)/(2 ÷ 2) = 50/1

(50 x 3)/(1 x 3) = 150/3

For the second blank :

(100 ÷ 2)/(2 ÷ 2) = 50/1  

(50 ÷ 2)/(1 ÷ 2) = 25/0.5

(25 x 7)/(0.5 x 7) = 175/3.5

For the third blank :

(100 x 2)/(2 x 2) = 200/4

Then, we have

Example 2 :

Look at the picture given below.

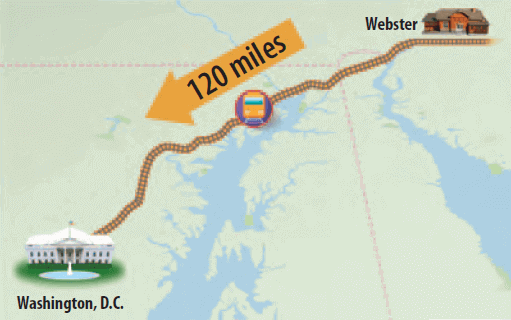
An express train travels from Webster to Washington, D.C., at a constant speed and makes the trip in 2 hours.

Question (i) :

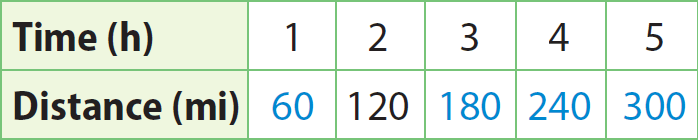
Make a table to show the distance the train travels in various amounts of time.

Answer :

Write a ratio of distance to time to find the rate.

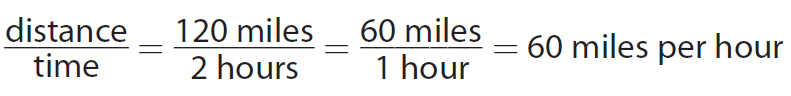
Use the unit rate to make a table.

Question (ii) :

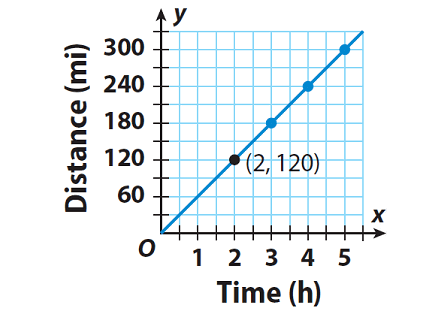
Graph the information from the table.

Answer :

Write ordered pairs with time as the x-coordinate and distance as the y-coordinate.

(1, 60), (2, 120), (3, 180), (4, 240), (5, 300)

Graph the ordered pairs. Fractions and decimals can represent times and distances, so connect the points.

Question (iii) :

Use the graph to find how long the train takes to travel 90 miles.

Answer :

When we look at the graph carefully, the value on y - axis which is corresponding to 1.5 on x-axis  is 90.

Look at the graph given below.

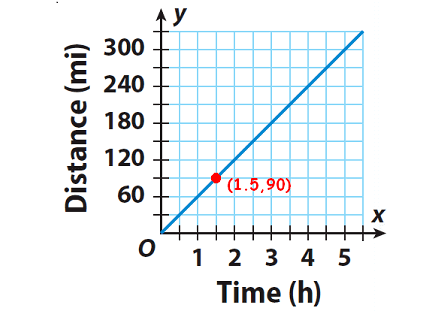
When we look at the above graph carefully, the value on y- axis which is corresponding to the value 1.5 on x-axis is 90.

The point (1.5, 90) is on the graph, so the train takes 1.5 hours.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.