RATIOS RATES TABLES AND GRAPHS WORKSHEET

Problem 1 :

Students in Mr. Webster’s science classes are doing an experiment that requires 250 milliliters of distilled water for every 5 milliliters of ammonia. The table shows the amount of distilled water needed for various amounts of ammonia.

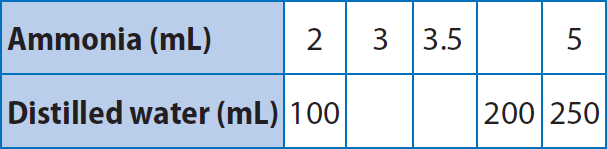
Questions : 

1. Use the numbers in the first column of the table to write a ratio of distilled water to ammonia.

2. How much distilled water is used for 1 milliliter of ammonia?

3.  Use your answer from question 2, write another ratio of distilled water to ammonia.

4. Check whether the two ratios from answers of question 1 and question 2 are equivalent or not equivalent. 

5. Complete the table. What are the equivalent ratios shown in the table ?

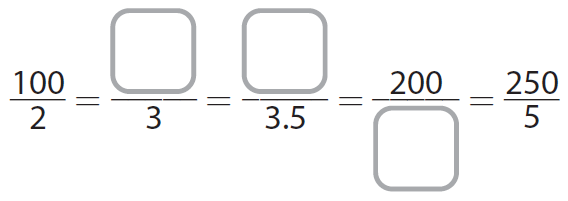
Problem 2 :

Look at the table and answer the questions given below. 

Questions :

1.  Write the information in the table as ordered pairs. Use the amounts of ammonia as the x-coordinates and the amounts of distilled water as the y-coordinates.

2.  What do you come to know from the graph ?

3.  For each ordered pair that you graphed, write the ratio of the y-coordinate to the x-coordinate.

4.  The ratio of distilled water to ammonia is

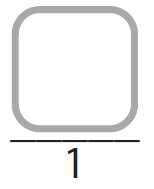
How are the ratios in question no.3 related to this ratio ?

5.  The point (2.5, 125) is on the graph below, but not in the table. 

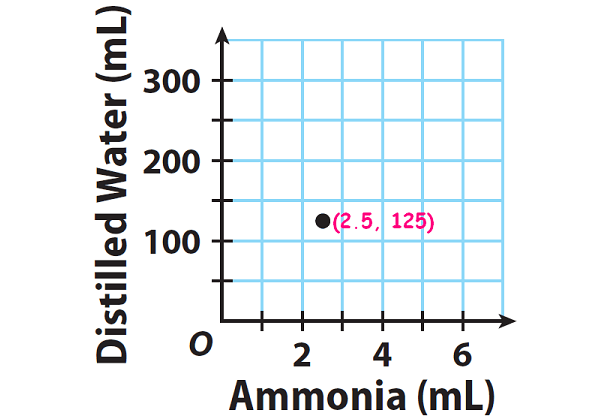
Find the ratio of the y-coordinate to the x-coordinate.

How is this ratio related to the ratios in question no.3 and 4 ?

6.  What do you think is true for every point on the graph ?

Answers

1. Solution :

(i). Answer :

100 ml distilled water/2 ml ammonia  (or)  100 : 2

(ii) Answer :

From the first column of the table, the ratio  of distilled water to ammonia is 

100 ml water/2 ml ammonia

To find the quantity of distilled water used for 1 milliliter of ammonia, we have to make the second quantity (ammonia) as 1. 

100 ml distilled water : 2 ml ammonia  =  (100 ÷ 2) / (2 ÷ 2)

100 ml distilled water : 2 ml ammonia  =  50 / 1

That is,

50 ml distilled water/1 ml ammonia  

The quantity of distilled water used for 1 milliliter of ammonia is 50 ml.

(iii) Answer :

To write another ratio from the answer of question 2, we have find an equivalent ratio to 50 : 1.

To find equivalent ratio of the given ratio, we have to multiply both the terms of the ratio by the same non zero number, say "2".

Then, we have 

(50x2) : (1x2) = 100 : 2

Therefore, another ratio of distilled water to ammonia is 100 : 2.

(iv) Answer :

The two ratios from the answers of question 1 and 2 are 

100 : 2 and 50 : 1 

Let us check, whether two rations 100 : 2 and 50 : 1 are equivalent or not equivalent.

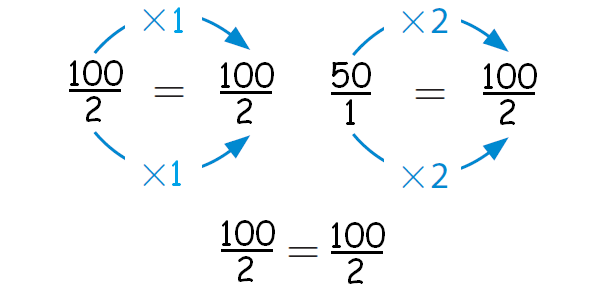
From the above working, it is clear that the two ratios 100 : 2 and 50 : 1 are equivalent.

(v) Answer :

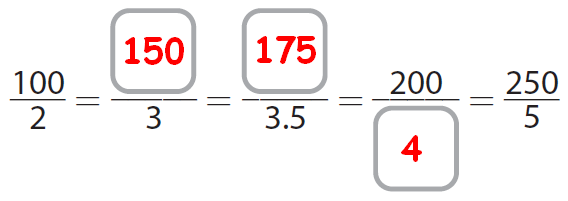
For the first blank :

(100 ÷ 2)/(2 ÷ 2) = 50/1

(50 x 3)/(1 x 3) = 150/3

For the second blank :

(100 ÷ 2)/(2 ÷ 2) = 50/1  

(50 ÷ 2)/(1 ÷ 2) = 25/0.5

(25 x 7)/(0.5 x 7) = 175/3.5

For the third blank :

(100 x 2)/(2 x 2) = 200/4

Then, we have

2. Solution :

(i) Answer :

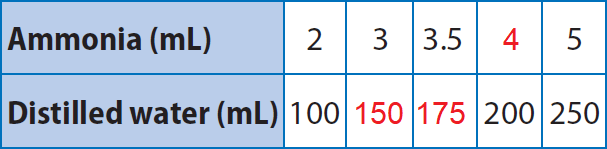
First, let us complete the given table.

From the first column, ratio between ammonia and distilled water is

For the first blank :

(2 ÷ 2)/(100 ÷ 2) = 1/50

(1 x 3)/(50 x 3) = 3/150

For the second blank :

(2 ÷ 2)/(100 ÷ 2) = 1/50

(1 ÷ 2)/(50 ÷ 2) = 0.5/25

(0.5 x 7)/(25 x 7) = 3.5/175

For the third blank :

(2 x 2)/(100 x 2) = 4/200

Let us write the ordered pairs in the form (x, y), where x represents ammonia and y represents distilled water. 

The ordered pairs from the above table are 

(2, 100), (3, 150), (3.5, 175), (4, 200), (5, 250)

Graph the ordered pairs.

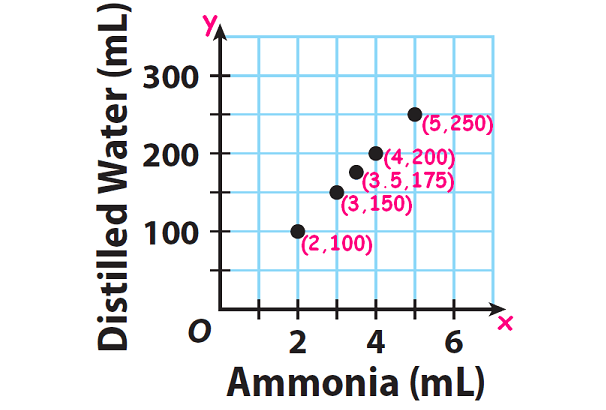
(ii) Answer :

From the above graph, it is clear that when the amount ammonia gets increased, the amount of distilled water also gets increased at the same rate.

(iii) Answer :

100/2,  150/3,  175/3.75,  200/4,  250/5

(iv) Answer :

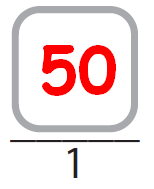
The ratio of distilled water to ammonia is

The above ratio is given between distilled water to ammonia. 

Let us find the above ratio.

Already we know the ratio between distilled water to ammonia.

That is, 

100/2

In the given ratio, the second quantity is 1. To make the second quantity 100/2 as 1, divide both the quantities by 2.

Then, we have 

(100 ÷ 2)/(2 ÷ 2)

The above ratio is between distilled water and ammonia. In questions no.3 also, all the ratios are between distilled water and ammonia.

Hence, all the ratios in question no.3 are equivalent to the ratio 50/1.

(v) Answer :

The ratio of the y-coordinate to the x-coordinate is

125 / 2.5  =  (125 x 10) / (2.5 x 10)

125 / 2.5  =  1250 / 25

125 / 2.5  =  (1250 ÷ 25)  / (25 ÷ 25)

125 / 2.5  =  50 / 1

This ratio 50/1 is between distilled water and ammonia. 

In questions no.3 and 4 also, all the ratios are between distilled water and ammonia.

Hence, all the ratios in question no.3 and 4 are equivalent to the ratio 50/1.

(vi) Answer :

From the points on the graph, it is true that there is 25 ml of distilled water for every 0.5 ml of ammonia. 

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.