RATIONALIZING THE DENOMINATOR WORKSHEET

Rationalize each denominator :

Problem 1 :

12/√6

Problem 2 :

√18/(3√2)

Problem 3 :

4√5/√10

Problem 4 :

5/√7

Problem 5 :

12/√72

Problem 6 :

(3 - √3)/√3

Problem 7 :

1/(3 + √2)

Problem 8 :

(1 - √5)/(3 + √5)

Problem 9 :

(√x + y)/(x - √y)

Problem 10 :

³√(2/3a)

1. Answer :

= 12/√6

Multiply both numerator and denominator by √6 to get rid of the radical in the denominator.

= (12 ⋅ √6)/(√6 ⋅ √6)

= 12√6/6

= 2√6

2. Answer :

= √18 / (3√2)

Simplify.

= √(3 ⋅ 3 ⋅ 2)/(3√2)

= 3√2/(3√2)

= 1

3. Answer :

= 4√5/√10

Simplify.

= 4√5/√(2 ⋅ 5)

= 4√5/(√2 ⋅ √5)

On the right side, cancel out √5 in numerator and denominator.

= 4/√2

On the right side, multiply both numerator and denominator by √2 to get rid of the radical in the denominator.

= (4 ⋅ √2)/(√2 ⋅ √2)

= 4√2/2

= 2√2

4. Answer :

= 5/√7

Multiply both numerator and denominator by √7 to get rid of the radical in the denominator.

= (5 ⋅ √7)/(√7 ⋅ √7)

= 5√7/7

5. Answer :

12/√72

Decompose 72 into prime factor using synthetic division. 

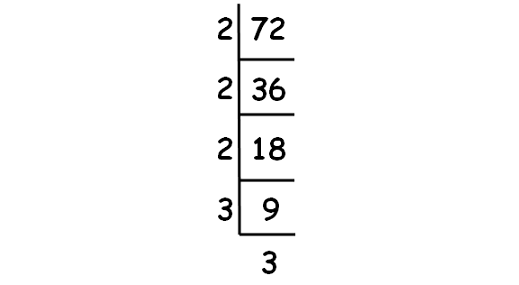
√72  =  √(2 ⋅ 2 ⋅ 2 ⋅ 3 ⋅ 3)

√72  =  2 ⋅ 3 ⋅ √2

√72  =  6√2

Then, we have

12/√72 = 12/6√2

Simplify.

= 2/√2

On the right side, multiply both numerator and denominator by √2 to get rid of the radical in the denominator.

= (2 ⋅ √2) ⋅ (√2 ⋅ √2)

= 2√2/2

= √2

6. Answer :

= (3 - √3)/√3

To get rid of the radical in denominator, multiply both numerator and denominator by √3.

= [(3-√3) ⋅ √3]/(√3 ⋅ √3)

= (3√3 - 3)/3

= 3(√3 - 1)/3

= √3 - 1

7. Answer :

= 1/(3 + √2)

To get rid of the radical in denominator, multiply both numerator and denominator by the conjugate of (3 + √2), that is by (3 - √2).

= [1 ⋅ (3-√2)]/[(3+√2) ⋅ (3-√2)]

= (3-√2)/[(3+√2) ⋅ (3-√2)]

Using the algebraic identity a² - b²  =  (a + b)(a - b), simplify the denominator on the right side.

= (3-√2)/[3² - (√2)²]

= (3-√2)/(9 - 2)

= (3 - √2)/7

8. Answer :

= (1 - √5)/(3 + √5)

To get rid of the radical in denominator, multiply both numerator and denominator by the conjugate of (3 + √5), that is by (3 - √5).

= [(1-√5) ⋅ (3-√5)]/[(3+√5) ⋅ (3-√5)]

Simplify.

= [3 - √5 - 3√5 + 5]/[3² - (√5)²]

= (8 - 4√5)/(9 - 5)

= 4(2 - √5)/4

= 2 - √5

9. Answer :

= (√x + y)/(x - √y)

To get rid of the radical in denominator, multiply both numerator and denominator by the conjugate of (x - √y), that is by (x + √y).

= [(√x + y) ⋅ (x + √y)]/[(x - √y) ⋅ (x + √y)]

Simplify.

= [x√x + √xy + xy + y√y]/[(x² - (√y)²]

= [x√x + √xy + xy + y√y]/(x² - y²)

10. Answer :

³√(2/3a) = ³√2/³√3a

To rationalize the denominator in this case, multiply both numerator and denominator on the right side by the cube root of 9a².

= [³√2 ⋅ ³√(9a²)]/[³√3a ⋅ ³√(9a²)]

Simplify.

= ³√(18a²)/³√(27a³)

= ³√(18a²)/³√(3 ⋅ 3 ⋅ 3 ⋅ a ⋅ a ⋅ a)

= ³√(18a²)/3a

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.