RATIONALIZING THE DENOMINATOR WORKSHEET
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Rationalize each denominator :
Problem 1 :
12/√6
Problem 2 :
√18/(3√2)
Problem 3 :
4√5/√10
Problem 4 :
5/√7
Problem 5 :
12/√72
Problem 6 :
(3 - √3)/√3
Problem 7 :
1/(3 + √2)
Problem 8 :
(1 - √5)/(3 + √5)
Problem 9 :
(√x + y)/(x - √y)
Problem 10 :
3√(2/3a)

1. Answer :
= 12/√6
Multiply both numerator and denominator by √6 to get rid of the radical in the denominator.
= (12 ⋅ √6)/(√6 ⋅ √6)
= 12√6/6
= 2√6
2. Answer :
= √18 / (3√2)
Simplify.
= √(3 ⋅ 3 ⋅ 2)/(3√2)
= 3√2/(3√2)
= 1
3. Answer :
= 4√5/√10
Simplify.
= 4√5/√(2 ⋅ 5)
= 4√5/(√2 ⋅ √5)
On the right side, cancel out √5 in numerator and denominator.
= 4/√2
On the right side, multiply both numerator and denominator by √2 to get rid of the radical in the denominator.
= (4 ⋅ √2)/(√2 ⋅ √2)
= 4√2/2
= 2√2
4. Answer :
= 5/√7
Multiply both numerator and denominator by √7 to get rid of the radical in the denominator.
= (5 ⋅ √7)/(√7 ⋅ √7)
= 5√7/7
5. Answer :
12/√72
Decompose 72 into prime factor using synthetic division.
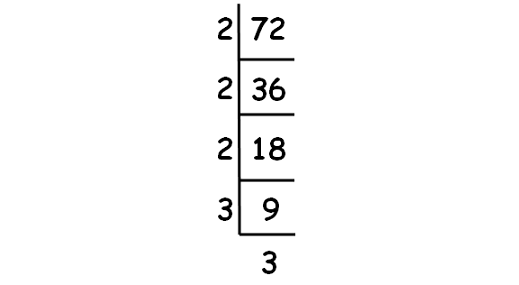
√72 = √(2 ⋅ 2 ⋅ 2 ⋅ 3 ⋅ 3)
√72 = 2 ⋅ 3 ⋅ √2
√72 = 6√2
Then, we have
12/√72 = 12/6√2
Simplify.
= 2/√2
On the right side, multiply both numerator and denominator by √2 to get rid of the radical in the denominator.
= (2 ⋅ √2) ⋅ (√2 ⋅ √2)
= 2√2/2
= √2
6. Answer :
= (3 - √3)/√3
To get rid of the radical in denominator, multiply both numerator and denominator by √3.
= [(3-√3) ⋅ √3]/(√3 ⋅ √3)
= (3√3 - 3)/3
= 3(√3 - 1)/3
= √3 - 1
7. Answer :
= 1/(3 + √2)
To get rid of the radical in denominator, multiply both numerator and denominator by the conjugate of (3 + √2), that is by (3 - √2).
= [1 ⋅ (3-√2)]/[(3+√2) ⋅ (3-√2)]
= (3-√2)/[(3+√2) ⋅ (3-√2)]
Using the algebraic identity a2 - b2 = (a + b)(a - b), simplify the denominator on the right side.
= (3-√2)/[32 - (√2)2]
= (3-√2)/(9 - 2)
= (3 - √2)/7
8. Answer :
= (1 - √5)/(3 + √5)
To get rid of the radical in denominator, multiply both numerator and denominator by the conjugate of (3 + √5), that is by (3 - √5).
= [(1-√5) ⋅ (3-√5)]/[(3+√5) ⋅ (3-√5)]
Simplify.
= [3 - √5 - 3√5 + 5]/[32 - (√5)2]
= (8 - 4√5)/(9 - 5)
= 4(2 - √5)/4
= 2 - √5
9. Answer :
= (√x + y)/(x - √y)
To get rid of the radical in denominator, multiply both numerator and denominator by the conjugate of (x - √y), that is by (x + √y).
= [(√x + y) ⋅ (x + √y)]/[(x - √y) ⋅ (x + √y)]
Simplify.
= [x√x + √xy + xy + y√y]/[(x2 - (√y)2]
= [x√x + √xy + xy + y√y]/(x2 - y2)
10. Answer :
3√(2/3a) = 3√2/3√3a
To rationalize the denominator in this case, multiply both numerator and denominator on the right side by the cube root of 9a2.
= [3√2 ⋅ 3√(9a2)]/[3√3a ⋅ 3√(9a2)]
Simplify.
= 3√(18a2)/3√(27a3)
= 3√(18a2)/3√(3 ⋅ 3 ⋅ 3 ⋅ a ⋅ a ⋅ a)
= 3√(18a2)/3a
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
10 Hard SAT Math Questions (Part - 44)
Jan 12, 26 06:35 AM
10 Hard SAT Math Questions (Part - 44) -
US Common Core K-12 Curricum Algebra Solving Simple Equations
Jan 07, 26 01:53 PM
US Common Core K-12 Curricum Algebra Solving Simple Equations -
10 Hard SAT Math Questions (Part - 4)
Jan 05, 26 06:56 PM
10 Hard SAT Math Questions (Part - 4)
