RATIONAL ZERO THEOREM WORKSHEET

Problem 1 :

State the possible rational zeros of f(x) and find all rational zeros. 

f(x)  =  5x³ + 29x² + 19x - 5

Problem 2 :

Use the Rational-Zero Theorem to find all rational zeros of

f(x)  =  4x⁴ + 3x³ + 4x² + 11x + 6

Problems 3-5 : State the possible rational zeros for each function.

Problem 3 :

f(x)  =  3x² + 2x - 1

Problem 4 :

f(x)  =  x⁶ - 64

Problem 5 :

f (x)  =  4x⁵ - 2x⁴ + 30x³ - 15x² + 50x − 25

Problems 6-8 : State the possible rational zeros for each function. Then find all rational zeros.

Problem 6 :

f(x)  =  x³ + x² - 5x + 3

Problem 7 :

f(x)  =  x³ - 13x² + 23x - 11

Problem 8 :

f (x)  =  3x³ + 11x² + 5x - 3

Problem 9 :

f (x)  =  4x⁵ - 2x⁴ + 30x³  - 15x² + 50x - 25

Problem 10 :

A box with open top is formed by cutting squares out of the corners of a rectangular piece of cardboard and then folding up the sides. IF x represents the length of the side of the square cut from each corner and if the original piece of cardboard is 16 inches by 9 inches, what size square must be cut if the volume of the box is to be 120 cubic inches ?

1. Answer :

The constant term is 5 and the leading coefficient is -5.

Factors of -5 : ±1, ±5

Factors of 5 : ±1, ±5

So, the possible rational zeros are 

±1/1, ±1/5, ±5/1, ±5/5

or

±1/1, ±1/5, ±5

Check 1 is rational zero to f(x).

f(1)  =  5(1)³ + 29(1)² + 19(1) - 5

=  5 + 29 + 19 - 5

=  5 + 29 + 19 - 5

=  48 ≠ 0

Check -1 is rational zero to f(x).

f(1)  =  5(-1)³ + 29(-1)² + 19(-1) - 5

=  -5 + 29 - 19 - 5

=  0

Check 1/5 is rational zero to f(x).

f(1/5)  =  5(1/5)³ + 29(1/5)² + 19(1/5) - 5

=  5(1/125) + 29(1/25) + 19/5 - 5

=  1/25 + 29/25 + 19/5 - 5

=  1/25 + 29/25 + 19/5 - 5

=  1/25 + 29/25 + 19/5 - 5

=  0

Check -1/5 is rational zero to f(x).

f(1/5)  =  5(-1/5)³ + 29(-1/5)² + 19(-1/5) - 5

=  5(-1/125) - 29(1/25) - 19/5 - 5

=  -1/25 - 29/25 - 19/5 - 5

=  -1/25 + 29/25 + 19/5 - 5

=  1/25 + 29/25 + 19/5 - 5

=  98/25 ≠ 0

Check 5 is rational zero to f(x).

f(5)  =  5(5)³ + 29(5)² + 19(5) - 5

=  625 + 725 + 95 - 5

=  1440 ≠ 0

Check -5 is rational zero to f(x).

f(-5)  =  5(-5)³ + 29(-5)² + 19(-5) - 5

=  -625 + 725 - 95 - 5

=  0

f(x) becomes zero when 

x  =  -5, -1, 1/5

So, the rational zeros of f(x) are -5, -1 and 1/5.

2. Answer :

The constant term is +6 and the leading coefficient is 4.

Factors of 6 : ±1, ±2, ±3, ±6

Factors of 4 : ±1, ±2, ±4

The possible rational zeros are 

±1, ±2, ±3, ±6, ±1/2, ±3/2, ±1/4, ±3/4

There are sixteen possible rational zeros. It's little hard to check each rational zero with f(x) as we have done in the previous problem. 

So, we can use the graph of the given function to find the actual rational zeros. 

The smallest possible rational zero is –6 and the largest is 6, so graph f on the interval –6 ≤ x ≤ 6 to see where rational zeros might be. 

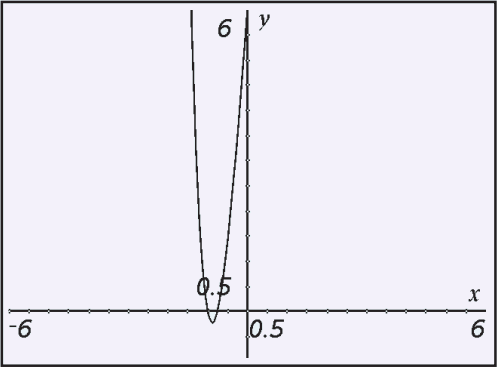
The graph above shows that there are two real zeros on the interval –1 ≤ x ≤ 0.

Use a graphing utility to find the x-intercepts of the graph of f(x).

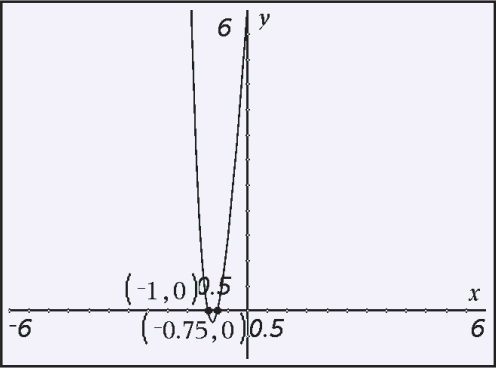
The possible rational zeros in the interval –1 ≤ x ≤ 0 are

-1/4, -1/2, -3/4, -1

Test these values with f(x). 

f(-1)  =  0

f(-3/4)  =  0

f(-1/2)  ≈  1.38

f(-1/4)  ≈  3.47

Hence, –1 and –3/4 are the only rational zeros of f(x).

Note : 

The Rational-Root Theorem identifies all possible rational roots of a polynomial with integer coefficients. So, any real roots that are not identified must be irrational.

3. Answer :

±1, ±1/3

4. Answer :

± 1, ± 2, ± 4, ± 8, ± 16, ± 32, ± 64

5. Answer :

± 1, ± 5, ± 25, ± 1/2 , ± 5/2 , ± 25/2 , ± 1/4 , ± 5/4 , ± 25/4

6. Answer :

Possible rational zeros : ± 1, ± 3

Rational zeros : {-3, 1 mult. 2}

7. Answer :

Possible rational zeros : ± 1, ± 11

Rational zeros : {1 mult. 2, 11}

8. Answer :

Possible rational zeros : ± 1, ± 3, ±1/3

Rational zeros : {1/3, -3, -1}

9. Answer :

f (x)  =  4x⁵ - 2x⁴ + 30x³  - 15x² + 50x - 25

The constant term is 25 and the leading coefficient is 4.

Factors of 4 : ±1, ±2, ±4

Factors of -25 : ±1, ±5, ±25

So, the possible rational zeros are 

±1/1, ±1/2, ±1/4, ±5/±1, ±5/±2, ±5/4, ±25/1, ±25/2, ±25/4

10. Answer :

Length of box = 16 inches

Width = 9 inches

Side length of corners = x

Length of cuboid = 16 - 2x

Width of cuboid = 9 - 2x

Height = x

Volume = 12

(16 - 2x)(9 - 2x) x = 120

(144 - 32x - 18x + 4x²)x = 120

4x³ - 50x² + 144x - 120 = 0

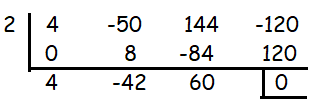
x = 2

4x² - 42x + 60 = 0

The remaining zeroes are rational numbers.

So, we cut by 2 x 2 square.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.