RATIONAL NUMBERS ON THE NUMBER LINE

A number line can be used to show the sets of natural number, whole numbers and integers.

Values greater than 0 or positive numbers, are listed to the right of 0, and values less than 0, or negative numbers, are listed to the left of 0.

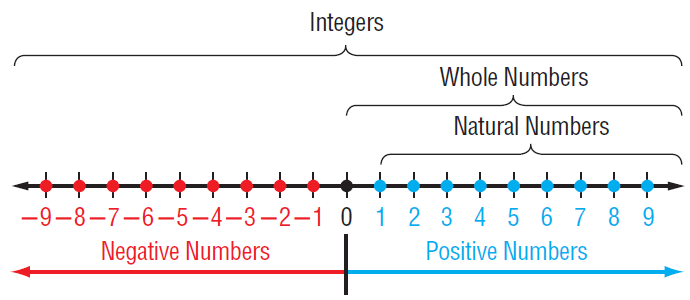
Another set of numbers you can display on a number line is the set of rational numbers.

A rational number is any number that can be written in the form ᵃ⁄b, where a and b are integers and b ≠ 0. Some examples of rational numbers are shown below.

½, ⁻²⁄₃, ¹⁷⁄₅, ¹⁵⁄₋₃, ⁻¹⁴⁄₋₁₁, ³⁄₁

A rational number can also be expressed as a decimal that terminates, or as a decimal that repeats indefinitely.

0.5, -0.333333.., 3.4, 2.6767… -5 1.2727.....,

- 1.23568994141…

Locating the rational numbers on a number line is an important skill. For example, to represent the number ⁻³⁄₄ on the number line, ⁻³⁄₄ being negative would be marked to the left of 0 and it is between 0 and -1. We know that the integers, 1 and –1 are equidistant from 0 and so are the numbers 2 and –2, 3 and –3 from 0.

This concept remains the same for rational numbers too. Now, as we mark ³⁄₄ to the right of zero, at 3 parts out of 4 between 0 and 1, the same way, we will mark ⁻³⁄₄ to the left of zero, at 3 parts out of 4 between 0 and –1 as shown below.

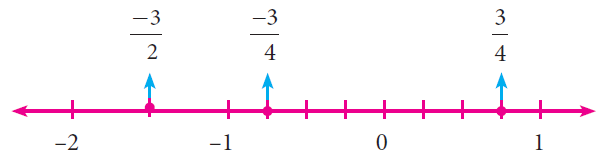
Similarly, it is easy to find ⁻³⁄₂ between -1 and -2, since

⁻³⁄₂ = -1½

Now, on the following number line what rational numbers do the letters A and B represent?

You will now be able to say easily the rational numbers marked by A and B on the number line as shown above. Isn’t it?

Here, A represents the rational number

-4⁴⁄₇ (or ⁻³²⁄₇)

and B represents the rational number

3⅗ (or ¹⁸⁄₅)

Example 1 :

Name the coordinates of the points graphed on each number line.

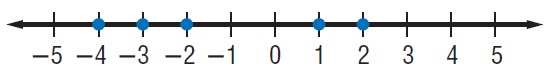
Solution :

The dots indicate each point on the graph. The coordinates are {-4, -3, -2, 1, 2}.

Example 2 :

Name the coordinates of the points graphed on each number line.

Solution :

The bold arrow on the right means that the graph continues indefinitely in that direction. The coordinates are {1, 1.5, 2, 2.5, 3, …}.

Example 3 :

Represent the set of numbers on the number line

{…-4, -2, 0, 2, 4, 6}

Solution :

The bold arrow on the right means that the graph continues indefinitely in that direction. 

Example 4 :

Represent the set of numbers on the number line

{⁻⁴⁄₃, ⁻¹⁄₃, ⅔, ⁵⁄₃}

Solution :

Example 5 :

Represent the set of numbers on the number line

{integers less than 3 or greater than or equal to 5}

Solution :

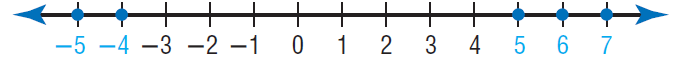
The bold arrow on the right means that the graph continues indefinitely in that direction. 

Example 6 :

Name the coordinates of the points graphed on each number line.

Solution :

The coordinates represented in the above graph are

{-2, 1, 2, 5}

Example 7 :

Name the coordinates of the points graphed on each number line.

Solution :

The coordinates represented in the above graph are

{⁻¹¹⁄₂, ⁻⁹⁄₂, ⁻⁷⁄₂, ⁻⁵⁄₂, ⁻³⁄₂}

Example 8 :

Represent the set of numbers on the number line

{-4, -2, 1, 5}

Solution :

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.