RATIONAL IRRATIONAL AND DECIMAL

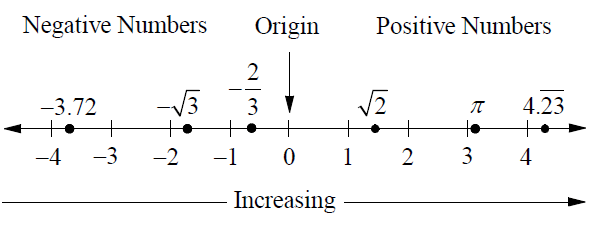
Numbers can be pictured as points on a horizontal line called a number line. The point for 0 is the origin. Points to the left of 0 represent negative numbers, and points to the right of 0 represent positive numbers. Numbers increase in value from left to right.

The point that corresponds to a number is called the graph of the number. Each number in a pair such as 3 and -3 is called the opposite of the other number. The opposite of 'a' is written '-a'.

Natural Numbers :

{1, 2, 3, ...........}

Whole Numbers :

{0, 1, 2, 3, ...........}

Integers :

{........... , -3, -2, -1, 0, 1, 2, 3, ...........}

Rational Numbers : 

A rational number is the one that can be expressed as a ratio a/b, where 'a' and 'b' are integers b ≠ 0. The decimal form of a rational number is either terminating or repeating decimal, such as 

-3.72, -2/3, 0.2 and 4.2323..........

Irrational Numbers : 

Any real number that is not rational is irrational.

-√3, √2 and π are irrational

√a is considered as irrational when 'a' is not a perfect square.

If you have square root of a number, it may be rational or irrational. To determine the square root of a number is rational or irrational, check the number inside the square root is a perfect square or NOT a perfect square.

If the number inside the square root is a perfect square, then the square root of the given number is rational.

If the number inside the square root is NOT a perfect square, then the square root of the given number is irrational.

For example.

√25 is a rational, because 25 is a perfect square

√25 = 5 (rational)

√10 is an irrational, because 10 is NOT a perfect square

√10 = 3.16227........ (irrational)

3.16227........ is a non terminating and non repeating decimal. So, 3.16227........ is an irrational number.

Rounding Decimals

To round a decimal to the desired place, underline the digit in the place to be rounded.

1. If the digit to the right of the underlined digit is 5 or more, increase the underlined digit by one (round up).

2. If the digit to the right of the underlined digit is less than 5, leave the underlined digit as it is (round down).

3. Drop all digits to the right of the underlined digit.

Solved Problems

Problem 1 :

On the number line below, the marks are equally spaced. What is the coordinate of P?

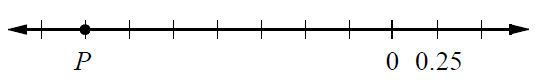
Solution :

Since the distance between the marks is 0.25, the coordinate of P is

= 70.25 x (-1.75)

= -1.75

Problem 2 :

Round 52.348 to the nearest

a) integer and b) hundredth.

Solution :

Part (a) :

Underline 2, the digit in the ones place. 52.348

The digit to the right of the underlined digit is less than 5, keep the underlined digit as it is.

Therefore, 52.348 rounded to the nearest integer is 52.

Part (b) :

Underline 4, the digit in the hundredths place. 52.348

The digit to the right of the underlined digit is more than 5, round up.

Therefore, 52.348 rounded to the nearest hundredths place is 52.35.

Problem 3 :

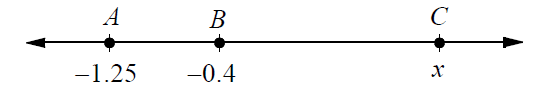
On the number line above, if BC = 2AB, then find the value of 'x'.

Solution :

BC = 2AB

C - B = 2(B - A)

x - (-0.4) = 2[-0.4 - (-1.25)]

x + 0.4 = 2(-0.4 + 1.25)

x + 0.4 = 2(0.85)

x + 0.4 = 1.7

Subtract 0.4 from both sides.

x = 1.3

Problem 4 :

Which of the following is an irrational number?

A) -1.2

B) 4/3

C) -√16

D) -√10

Solution :

A) -1.2 :

-1.2 = -12/10

= -6/5

-6/5 is in the form of a/b

-1.2 is a rational number.

B) 4/3 :

4/3

4/3 is in the form of a/b

4/3 is a rational number.

C) -√16 :

-√16 = -4

= -4/1

-4/1 is in the form of a/b

-√16 is a rational number.

D) -√10 :

-√10 = -3.16227.........

-3.16227 is a non terminating and non repeating decimal.

-√10 is an irrational number.

The correct answer choice is (D) -√10.

Problem 5 :

Which of the following is a rational number?

A) √1.6

B) -√250

C) √0.9

D) √(49/64)

Solution :

A) √1.6 :

16 is a perfect square. But 1.6 is not a perfect square.

4² = 16, but

(0.4)² = 0.4 x 0.4 = 0.16 

(0.4)² ≠ 1.6

Since the number 1.6 inside the square root is not a perfect square, √1.6 is an irrational number.

B) -√250 :

We know that 225 (= 15²) is a perfect square  and the next perfect square is 289 (= 17²). Any number between 225 and 289 can not be a perfect square. So, 250 is not a perfect square.  

Since the number 250 inside the square root is not a perfect square, √250 is an irrational number.

C) √0.9 :

9 is a perfect square. But 0.9 is not a perfect square.

3² = 9, but

(0.3)² = 0.3 x 0.3 = 0.09 

(0.3)² ≠ 0.9

Since the number 0.9 inside the square root is not a perfect square, √0.9 is an irrational number.

D) √(49/64) :

√(49/64) = √49/√64

= 7/8

7/8 is in the form of a/b

√(49/64) is a rational number.

The correct answer choice is (D) √(49/64).

Problem 6 :

Find the number which is halfway between -5/6 and 1/3 on a number line.

Solution :

To find a number on a number line which is halfway between two numbers, find the average of the two numbers.

Average of -5/6 and 1/3 = (-5/6 + 1/3) ÷ 2

= (-5/6 + 2/6) ÷ 2

= (-5 + 2)/6 ÷ 2

 = -3/6 ÷ 2

= -1/2 ÷ 2

= -1/2 x 1/2

= -1/4

On a number line, -1/4 is a number between -5/6 and 1/3.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.