RATIONAL AND IRRATIONAL NUMBERS

First let us come to know, what is rational number. Because, once we understand rational number, we can easily understand irrational number.

A rational number has to be in the form as given below.

Rational Numbers

So, any number in the form of fraction can be treated as rational number.

Examples of Rational Number :

5, 2.3, 0.02, 5/6

Because all these numbers can be written as fractions.

5 = 5/1

2.3 = 23/10

0.02 = 2/100 = 1/50

5/6 (This is already a fraction)

Apart from the above examples, sometimes we will have recurring decimals like 1.262626..........

1.262626........ is a non terminating recurring decimal.

All these recurring decimals can be converted to fractions and they are also rational numbers.

Irrational Numbers

A number which can not be converted into fraction is called as irrational numbers.

Examples of Irrational Number :

All the above non terminating numbers can not be converted to fractions.

Because, they do not have repeated patterns.

When we are trying to find square of a number which is not a perfect square, we get this non repeating non terminating decimal.

And these non recurring decimals can never be converted to fractions and they are called as irrational numbers.

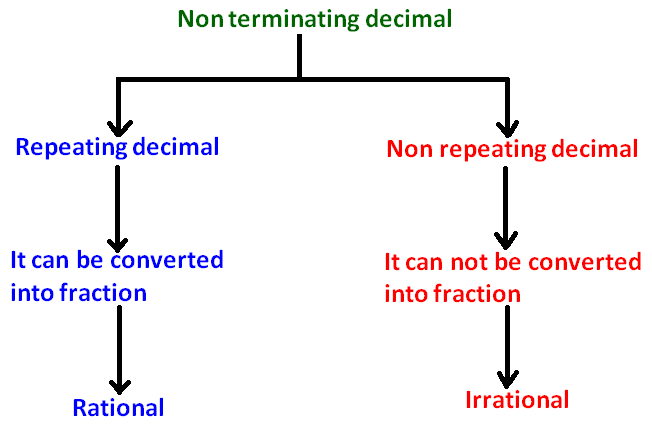
Difference between Rational and Irrational Numbers

Difference between rational and irrational numbers has been clearly explained in the picture given below.

Example :

Rational : 1.2626262626..........(Repeated pattern is 26)

Irrational : 1.4142135623..............(No repeated pattern)

More clearly,

A non terminating decimal which has repeated pattern is called as rational number.

Because, the non terminating decimal which has repeated pattern can be converted into fraction.

A non terminating decimal which does not have repeated pattern is called as irrational number.

Because, the non terminating decimal which does not have repeated pattern can not be converted into fraction.

Now, our question is, how a non terminating decimal which has repeated pattern can be converted to fraction. That we are going to see in the next section.

How to convert non-terminating and repeating decimal to fraction ?

Step 1 :

Let x = 2.0343434...........

Step 2 :

Identify the repeated pattern

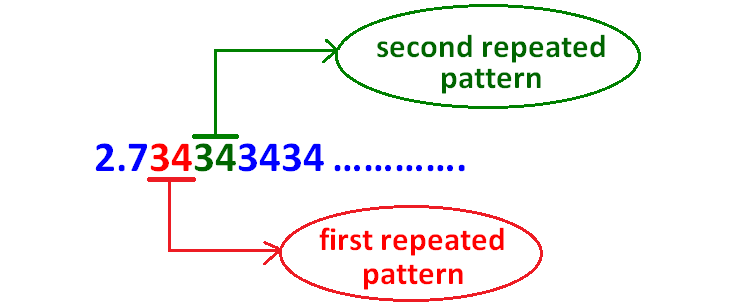
In 2.0343434..........., the repeated pattern is 34

(Because 34 is being repeated)

Step 3 :

Identify the first repeated pattern and second repeated pattern as as explained below.

Step 4 :

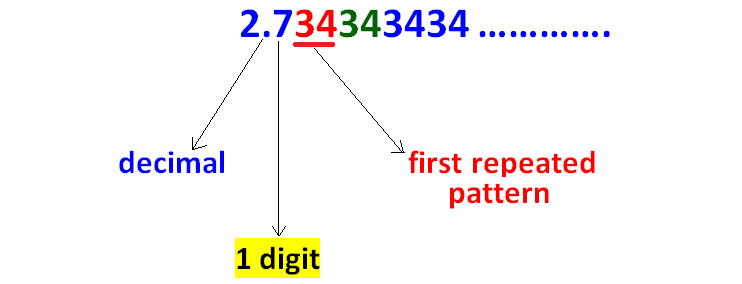
Count the number of digits between the decimal point and first repeated pattern as given in the picture below.

Step 5 :

Since there is 1 digit between the decimal point and the first repeated pattern, we have to multiply the given decimal by 10 as given in the picture below.

(If there are two digits -----------> multiply by 100,

three digits -----------> multiply by 1000 and so on )

Note :

In (1), we have only repeated patterns after the decimal.

Step 6 :

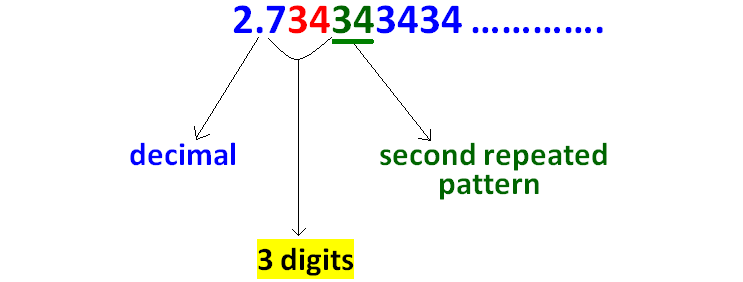
Count the number of digits between the decimal point and second repeated pattern as given in the picture below.

Step 7 :

Since there are 3 digits between the decimal point and the second repeated pattern, we have to multiply the given decimal by 1000 as given in the picture below.