RATIO RATES AND PROPORTIONS
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Ratio and Proportion
A ratio is a comparison of two quantities by division. The ratio of a to b can be written a : b or ᵃ⁄b, where b ≠ 0.
Ratios that name the same comparison are said to be equivalent. A statement that two ratios are equivalent, such as ¹⁄₁₂ = ²⁄₂₄ , is called a proportion.
Using Ratios
Example 1 :
The ratio of faculty members to students at a college is 1:15. There are 750 students. How many faculty members are there?
Solution :
Write a ratio comparing faculty to students.
Faculty ----> 1
Students ----> 15
Write a proportion. Let x be the number of faculty members.
ˣ⁄₇₅₀ = ¹⁄₁₅
Because x is divided by 750, multiply each side of the equation by 750.
750 ⋅ (ˣ⁄₇₅₀) = (¹⁄₁₅) ⋅ 750
x = 50
There are 45 faculty members.
Rates
A rate is a ratio of two quantities with different units, such as 48 mi/3 gal. Rates are usually written as unit rates. A unit rate is a rate with a second quantity of 1 unit, such as 16 mi/1 gal, or 16 mi/gal. You can convert any rate to a unit rate.
Finding Unit Rates
Example 2 :
David ate 58.5 hot dogs in 13 minutes to win a contest. Find the unit rate in hot dogs per minute. Round to the nearest hundredth.
Solution :
Write a proportion to find an equivalent ratio with a second quantity of 1.
⁵⁸.⁵⁄₁₃ = ˣ⁄₁
4.5 = x
The unit rate is approximately 4.46 hot dogs per minute.
Dimensional Analysis
Dimensional analysis is a process that uses rates to convert measurements from one unit to another. A rate such as 12 in./1 ft, in which the two quantities are equal but use different units, is called a conversion factor . To convert from one set of units to another, multiply by a conversion factor.
Using Dimensional Analysis
Example 3 :
A large adult male human has about 12 pints of blood. Use dimensional analysis to convert this quantity to gallons.
Solution :
Step 1 :
Convert pints to quarts.
Multiply by a conversion factor whose first quantity is quarts and whose second quantity is pints.
12 pt ⋅ (1 qt/2 pt) = 6 qt
12 pints is 6 quarts.
Step 2 :
Convert quarts to gallons.
Multiply by a conversion factor whose first quantity is gallons and whose second quantity is quarts.
6 qt ⋅ (1 gal/4 qt) = 6/4 gal = 1½ gal
A large adult male human has about 1½ gallons of blood.
Example 4 :
The dwarf sea horse Hippocampus zosterae swims at a rate of 52.68 feet per hour. Use dimensional analysis to convert this speed to inches per minute.
Solution :
1 foot = 12 inches
1 hour = 60 minutes
Use the above conversion factors to convert feet to inches and hours to minutes.
52.68 ft ⋅ 12 in. = 632.16 in.
1 hr ⋅ 60 min = 60 min
Then,
The speed is 10.536 inches per minute.
Cross Products
In the proportion ᵃ⁄b = ᶜ⁄d, the products a · d and b · c are called cross products.
You can solve a proportion for a missing value by using the Cross Products Property.
Cross Products Property
Words :
In a proportion, cross products are equal.
Numbers :
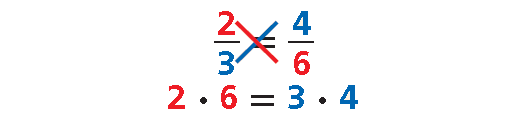
Algebra :
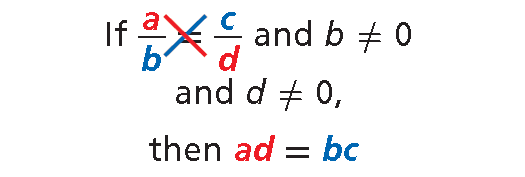
Solving Proportions
Solve each proportion.
Example 5 :
⁷⁄₉ = ³⁄ₓ
Solution :
⁷⁄₉ = ³⁄ₓ
Use cross products.
7x = 3(9)
7x = 27
Divide each side by 7.
x = 27/7
Example 6 :
⁵⁄₉ = ¹⁰⁄₍ₓ ₊ ₂₎
Solution :
⁵⁄₉ = ¹⁰⁄₍ₓ ₊ ₂₎
Use cross products.
5(x + 2) = 9(10)
5x + 10 = 90
Subtract 10 from each side.
5x = 80
Divide each side by 5.
x = 16
Scale Drawings and Scale Models
A scale is a ratio between two sets of measurements, such as 1 in : 7 mi. A scale drawing or scale model uses a scale to represent an object as smaller or larger than the actual object. A map is an example of a scale drawing.
Example 7 :
On a map with a scale of 1 in = 18 mi, the distance from Chicago to Evanston is 0.63 in. What is the actual distance ?
Solution :
Write the scale as a fraction.
map/actual = 1 in/18 mi
Let x be the actual distance.
¹⁄₁₈ = ⁰.⁶³⁄ₓ
Use cross products to solve.
1(x) = 18(0.63)
x = 11.34 miles
The actual distance is 11.34 miles.
Example 8 :
The actual distance between the two cities A and B is 54 mi. Find this distance on a map with a scale of 1 in = 18 mi. Round to the nearest tenth.
Solution :
Write the scale as a fraction.
map/actual = 1 in/ 18 mi
Let x be the distance on a map.
ˣ⁄₅₄ = ¹⁄₁₈
Use cross products to solve.
18(x) = 54(1)
18x = 54
Divide each side by 18.
18x/18 = 54/18
x = 3
The distance on the map is 3 inches.
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com
Recent Articles
-
Specifying Units of Measure
Dec 15, 25 07:09 PM
Specifying Units of Measure -
Quantitative Reasoning Questions and Answers
Dec 14, 25 06:42 AM
Quantitative Reasoning Questions and Answers -
Coin Tossing Probability
Dec 13, 25 10:11 AM
Coin Tossing Probability - Concept - Sample Space - Formula - Solved Problems