RATIO AND PROPORTION WORKSHEET WITH ANSWERS
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Question 1 :
Simplify the ratio :
16 cm : 4 m
Question 2 :
Simplify the ratio :
12 ft : 24 in.
Question 3 :
Find the ratio of 2 hours and 115 minutes.
Question 4 :
Find the ratio of $2.8 and $1.4.
Question 5 :
The length and width of a rectangle is in the ratio 3 : 5. If its perimeter is 48 cm, find its length and width.
Question 6 :
If $1000 is divided among the three people in the ratio 2:3:5, find the share of each.
Question 7 :
Find the inverse ratio of 12 : 13.
Question 8 :
If x : 2 and 5 : 6 are inverse to each other, find the value of x.
Question 9 :
Two numbers are in the ratio 2 : 3. If 4 be subtracted from each, they are in the ratio 3 : 5. Find the numbers.
Question 10 :
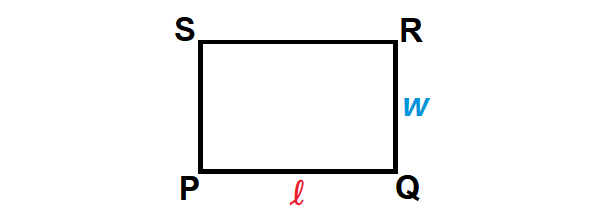
The perimeter of rectangle PQRS shown below is 60 centimeters. The ratio of PQ : QR is 3 : 2. Find the length and width of the rectangle.
Question 11 :
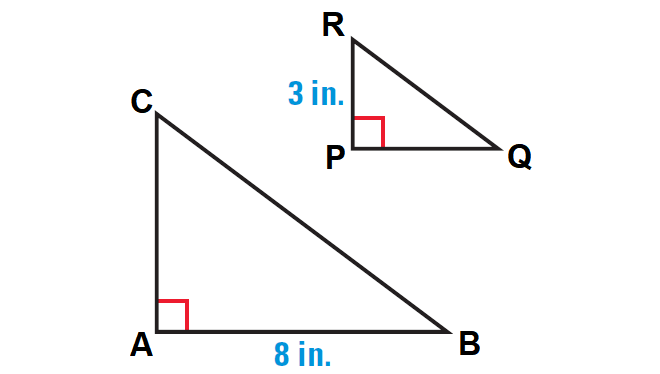
The ratios of the side lengths of ΔABC to the corresponding side lengths of ΔPQR are 2 : 1. Find the unknown lengths.
Question 12 :
The measure of the angles in ABC are in the extended ratio of 1 : 2 : 3. Find the measures of the angles.
Question 13 :
Solve the proportion :
6 : x = 12 : 5
Question 14 :
Solve the proportion :
3 : (p + 2) = 2 : p
Question 15 :
The photo below shows a painting. The actual painting is 12 inches high. How wide is it?
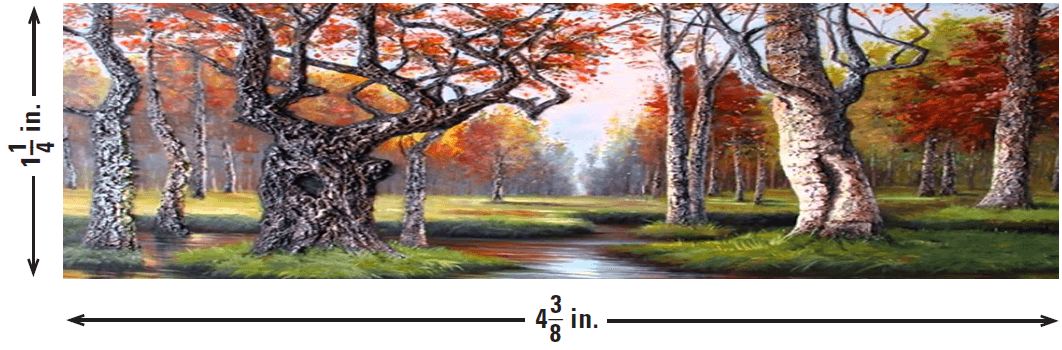
Question 16 :
P, Q and R are three cities. The ratio of average temperature between P and Q is 11 : 12 and that between P and R is 9 : 8. Find the ratio of P : Q : R.
Question 17 :
Kevin $80 in 7 hours and Peter earns $90 in 12 hours. Find the ratio of their earnings.
Question 18 :
The ratio between the speeds of two cars is 4 : 5 and the second car runs 250 miles in 5 hours, find the speed of the first car.

Answers
1. Answer :
To simplify ratios with unlike units, convert to like units so that the units divide out. Then simplify the fraction, if possible.
= 16 cm : 4 m
= 16 cm : 4 ⋅ 100 cm
= 16 cm : 400 cm
= 16 : 400
= ¹⁶⁄₁₆ : ⁴⁰⁰⁄₁₆
= 1 : 25
2. Answer :
The given two quantities are in different units.
That is, the first one is in feet and the second in inches.
As we did in the first problem, we can convert them into like units and then simplify the fraction, if possible.
= 12 ft : 24 in.
= 12 ⋅ 12 in. : 24 in.
= 144 in. : 24 in.
= 144 : 24
= ¹⁴⁴⁄₂₄ : ²⁴⁄₂₄
= 6 : 1
3. Answer :
= 2 hrs : 115 min
= 2 ⋅ 60 min = 115 min
= 120 min = 115 min
= 120 : 115
= ¹²⁰⁄₅ : ¹¹⁵⁄₅
= 24 : 23
So, the ratio of 2 hours and 115 minutes is 24 : 23.
4. Answer :
= $2.8 : $1.4
= 2.8 : 1.4
= (2.8 ⋅ 10) : (1.4 ⋅ 10)
= 28 : 14
= ²⁸⁄₁₄ : ¹⁴⁄₁₄
= 2 : 1
5. Answer :
From the given ratio, we have
length = 3x
width = 5x
Perimeter = 48
2(l + w) = 48
2(3x + 5x) = 48
8x = 24
x = 3
Therefore,
length = 3(3) = 9 cm
width = 5(3) = 15 cm
6. Answer :
Share of the first person = 2x.
Share of the second person = 3x.
Share of the third person = 5x.
Total Amount = $1000
2x + 3x + 5x = 1000
10x = 1000
x = 100
Therefore,
share of the first person = 2(100) = $200
share of the second person = 3(100) = $300
share of the third person = 5(100) = $500
7. Answer :
The inverse ratio of 12 : 13 is 13 : 12.
8. Answer :
Because the given two ratios are inverse to each other, the product of the two ratios is equal 1.
(x : 2) ⋅ (5 : 6) = 1
ˣ⁄₂ ⋅ ⅚ = 1
⁵ˣ⁄₁₂ = 1
x = ¹²⁄₅
9. Answer :
From the given ratio 2 : 3, we have
first number = 2x
second number = 3x
From the information "If 4 be subtracted from each, they are in the ratio 3:5", we have
(2x - 4) : (3x - 4) = 3:5
Using cross product rule of proportion, we have
5(2x - 4) = 3(3x - 4)
10x - 20 = 9x - 12
x = 8
Therefore,
the first number = 2(8) = 16
the second number = 3(8) = 24
10. Answer :

Because the ratio of PQ : QR is 3 : 2, we can represent the length PQ as 3x and the width QR as 2x.
2l + 2w = p
Substitute l = 3x and w = 2x.
2(3x) + 2(2x) = 60
Simplify.
6x + 4x = 60
10x = 60
Divide both sides by 10.
x = 6
length = 3 ⋅ 6 = 18 cm
width = 2 ⋅ 6 = 12 cm
Hence, rectangle PQRS has a length of 18 centimeters and a width of 12 centimeters.
11. Answer :

From the given information and the diagram shown above, we can consider the following points.
AB is twice PQ and AB = 8. So
PQ = ½ ⋅ 8 = 4 in.
PQ = 4 in.
Using the Pythagorean Theorem, we can determine that QR = 5.
AC is twice PR and PR = 3. So
AC = 2 ⋅ 3
AC = 6 in.
BC is twice QR and QR = 5. So,
BC = 2 ⋅ 5 = 10 in.
12. Answer :
Begin by sketching a triangle. Then use the extended ratio of 1 : 2 : 3 to label the measures of the angles as x°, 2x°, and 3x°.
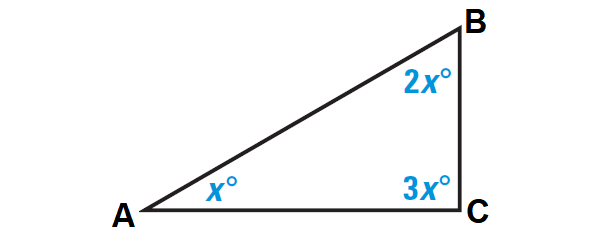
By Triangle Sum Theorem,
x° + 2x° + 3x° = 180°
x + 2x + 3x = 180
Simplify.
6x = 180
Divide both sides by 6.
x = 30
x° = 30°
2x° = 2 ⋅ 30° = 60°
3x° = 3 ⋅ 30° = 90°
Hence, the angle measures are 30°, 60° and 90°.
13. Answer :
Write the original proportion.
6 : x = 12 : 5
By cross product property, we have
6 ⋅ 5 = x ⋅ 12
30 = 12x
Divide both sides by 12.
⁵⁄₂ = x
14. Answer :
Write the original proportion.
3 : (p + 2) = 2 : p
By cross product property, we have
3p = 2(p + 2)
3p = 2p + 4
Subtract 2p from both sides.
p = 4
15. Answer :
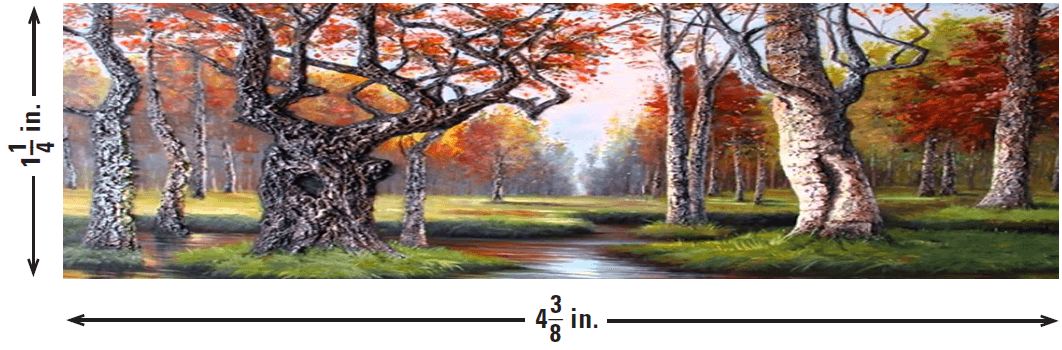
We can reason that in the photograph all measurements of the artist’s painting have been reduced by the same ratio.
That is, the ratio of the actual width to the reduced width is equal to the ratio of the actual height to the reduced height.
The photograph is 1¼ inches by 4⅜ inches.
Problem Solving Strategy :
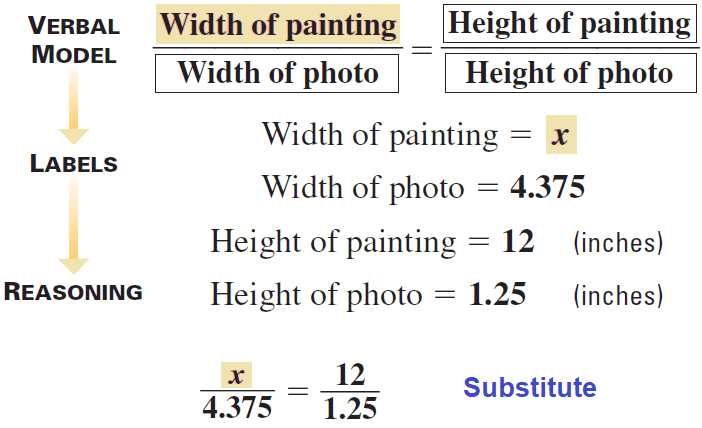
Multiply both sides by 4.375.
4.375(ˣ⁄₄.₃₇₅) = (¹²⁄₁.₂₅)4.375
x = 42
So, the actual painting is 42 inches wide.
16. Answer :
P : Q = 11 : 12
Q : R = 9 : 8
In the above two ratios, we find Q in common.
The value corresponding to Q in the first ratio is 12 and that of the second ratio is 9.
We have to get the same value for Q in both the ratios.
The least common multiple of (12, 9) is 36.
|
P : Q = (11 ⋅ 3) : (12 ⋅ 3) P ; Q : 33 : 36 |
Q : R = (9 ⋅ 4) : (8 ⋅ 4) Q : R = 36 : 32 |
In the both the ratios above, the value corresponding to Q is same, that is 36.
Therefore,
P : Q : R = 33 : 36 : 32
17. Answer :
Kevin earns $80 in 7 hours
Peter earns $90 in 12 hours
The earnings of Kevin and Peter are given for different time periods. That is, 7 hours and 12 hours.
To find the ratio of their earnings, we have to convert the earnings to the same time period, that is for 1 hour.
Earning of Kevin in 1 hour (in dollars) :
= ⁸⁰⁄₇
Earning of Peter in 1 hour (in dollars):
= ⁹⁰⁄₁₂
= ¹⁵⁄₂
The ratio of their earnings :
= ⁸⁰⁄₇ : ¹⁵⁄₂
The least common multiple of (7, 2) is 14. Multiply both the terms of the ratio by 14 to get rid of the denominators.
= (14 ⋅ ⁸⁰⁄₇) : (14 ⋅ ¹⁵⁄₂)
= 160 : 105
= ¹⁶⁰⁄₅ : ¹⁰⁵⁄₅
= 32 : 21
18. Answer :
From the given ratio 4 : 5, we have
speed of the first car = 4x ----(1)
speed of the second car = 5x ----(2)
Second car runs 250 miles in 5 hours (given).
speed = ᵈⁱˢᵗᵃⁿᶜᵉ⁄tᵢmₑ
So, speed of the second car is
= ²⁵⁰⁄₅
= 50 mph ----(3)
From (2) and (3), we get
5x = 50
x = 10
From (1), speed of the first car is
= 4x
= 4 ⋅ 10
= 40 mph
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
10 Hard SAT Math Questions (Part - 44)
Jan 12, 26 06:35 AM
10 Hard SAT Math Questions (Part - 44) -
US Common Core K-12 Curricum Algebra Solving Simple Equations
Jan 07, 26 01:53 PM
US Common Core K-12 Curricum Algebra Solving Simple Equations -
10 Hard SAT Math Questions (Part - 4)
Jan 05, 26 06:56 PM
10 Hard SAT Math Questions (Part - 4)
