RATE OF CHANGE AND SLOPE WORKSHEET

Problem 1 :

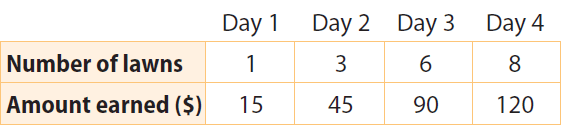
Eve keeps a record of the number of lawns she has mowed and the money she has earned. Tell whether the rates of change are constant or variable.

Problem 2 :

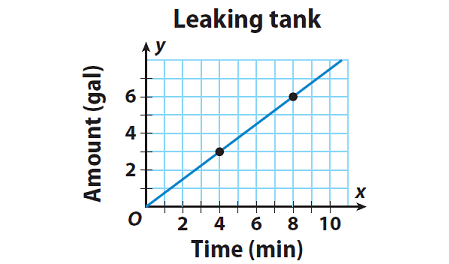
The graph shows the rate at which water is leaking from a tank. The slope of the line gives the leaking rate in gallons per minute. Find the slope of the line.

Problem 3 :

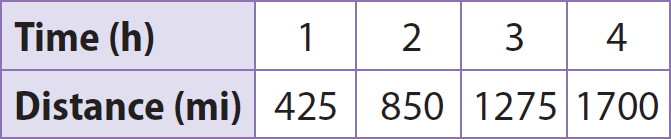
The equation y = 375x represents the relationship between x, the time that a plane flies in hours, and y, the distance the plane flies in miles for Plane A. The table represents the relationship for Plane B. Find the slope of the graph for each plane and the plane’s rate of speed. Determine which plane is flying at a faster rate of speed.

Problem 4 :

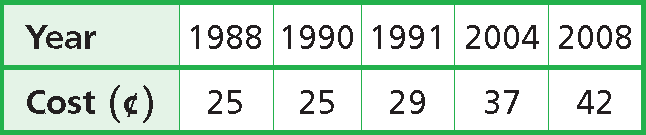
The table shows the cost of mailing a 1-ounce letter in different years. Find the rate of change in cost for each time interval. During which time interval did the cost increase at the greatest rate?

Answers

1. Answer :

Step 1 :

Identify the independent and dependent variables.

Independent : Number of lawns

Dependent : Amount earned

Step 2 :

Find the rates of change.

Day 1 to Day 2 :

Change in $/Change in lawns  =  (45 - 15)/(3 - 1)

=  30/2 

=  15

Day 2 to Day 3 :

Change in $/Change in lawns  =  (90 - 45)/(6 - 3)

=  45/3

=  15

Day 3 to Day 4 :

Change in $/Change in lawns  =  (120 - 90)/(8 - 6)

=  30/2

=  15

The rates of change are constant : $15 per lawn.

2. Answer :

Step 1 :

Choose two points on the line.

P(x₁, y₁)  =  P(4, 3)

Q(x₂, y₂)  =  Q(8, 6)

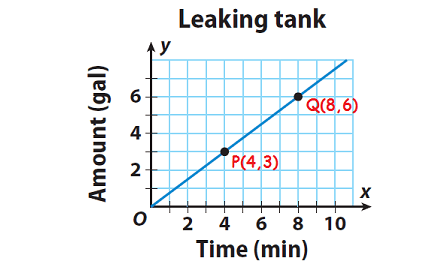
Step 2 :

Find the change in y-values (rise  =  y₂ - y₁) and the change in x-values (run  =  x₂ - x₁) as you move from one point to the other.

rise  =  y₂ - y₁     run  =  x₂ - x₁

rise  =  3 - 6     run  =  4 - 8

rise  =  -3     run  =  -4

Step 3 :

m  =  rise/run

m  = (y₂ - y₁)/(x₂ - x₁)

m  =  (-3)/(-4)

m  =  3/4

3. Answer :

Step 1 :

Use the equation y  =  375x to find the slope of the graph of Plane A.

Slope  =  Unit rate

Here, unit rate is the distance covered by the plane in one hour.

To find unit rate, plug x  =  1 in y  =  375x

Slope  =  375(1) 

Slope  =  375 miles/hour

Step 2 :

Use the table to find the slope of the graph of Plane B.

Slope  =  Unit rate 

Slope  =  (850 - 425)/(2 - 1) 

Slope  =  425/1

Slope  =  425 miles/hour.

Step 3 :

Compare the unit rates.

425 > 375

So, Plane B is flying faster.  

4. Answer :

Step 1 :

Identify the dependent and independent variables.

dependent : cost; independent : year

Step 2 :

Find the rates of change.

Rate of change : change in cost / change in years

1988 to 1990 : 

=  (25 - 25)/(1990 - 1988)

=  0/2

=   0

=  0  cents/year

1990 to 1991 : 

=  (29 - 25)/(1991 - 1990)

=  4/1

=   4

=  4  cents/year

1991 to 2004 : 

=  (37 - 29)/(2004 - 1991)

=  8/13

≈  0.62

≈  0.62 cents/year

2004 to 2008 : 

=  (42 - 37)/(2008 - 2004)

=  5/4

=  1.25

  =  1.25 cents/year

The cost increased at the greatest rate from 1990 to 1991.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.