SOLVING SYSTEM OF LINEAR EQUATIONS BY RANK METHOD
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Step 1 :
Find the augmented matrix [A, B] of the system of equations.
Step 2 :
Find the rank of A and rank of [A, B] by applying only elementary row operations.
Note :
Column operations should not be applied.
Step 3 :
Case 1 :
If there are n unknowns in the system of equations and
ρ(A) = ρ([A|B]) = n
then the system AX = B, is consistent and has a unique solution.
Case 2 :
If there are n unknowns in the system AX = B
ρ(A) = ρ([A| B]) < n
then the system is consistent and has infinitely many solutions and these solutions.
Case 3 :
If ρ(A) ≠ ρ([A| B])
then the system AX = B is inconsistent and has no solution.
Example 1 :
Solve the following linear equation by rank method
2x + 5y + 7z = 52
x + y + z = 9
2x + y - z = 0
Solution :
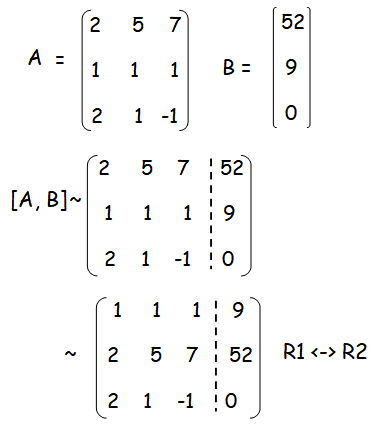
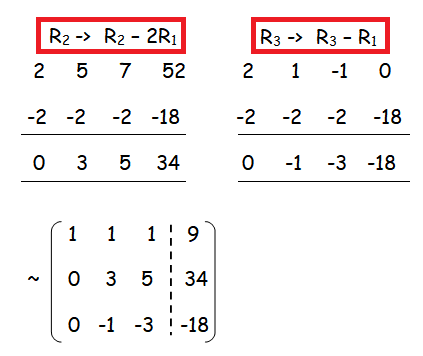
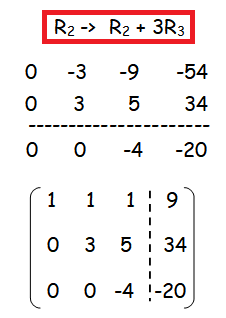
Number of non zero rows are 3.
ρ(A) = ρ([A|B]) = 3. The system is consistent and it has unique solution.
From 1st row,
x + y + z = 9 -----(1)
From 2nd row,
3y + 5z = 34 -----(2)
From 3rd row,
-4z = -20 -----(3)
From (3)
z = 5
By applying the value of z in (2), we get
3y + 5(5) = 34
3y + 25 = 34
3y = 34-25
3y = 9
y = 3
By applying the value of y and z in (1), we get
x + 3 + 5 = 9
x + 8 = 9
x = 1
So, the solution is (1, 3, 5).
Example 2 :
Solve the following linear equation by rank method
4x - 2y + 5z = 6
3x + 3y + 8z = 4
x - 5y - 3z = 5
Solution :
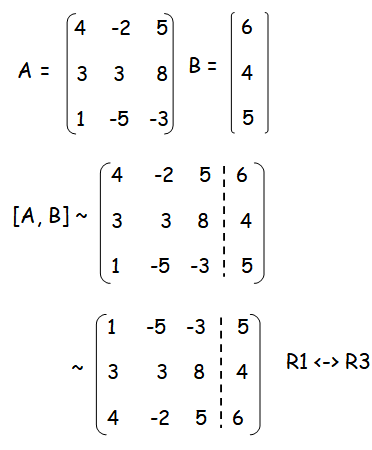

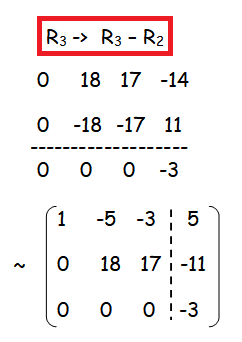
ρ(A) = 2 and ρ([A|B]) = 3. The system is inconsistent and it has no solution.
Example 3 :
Solve the following linear equation by rank method
x + 9y - z = 27
x - 8y + 16z = 10
2x + y + 15z = 37
Solution :
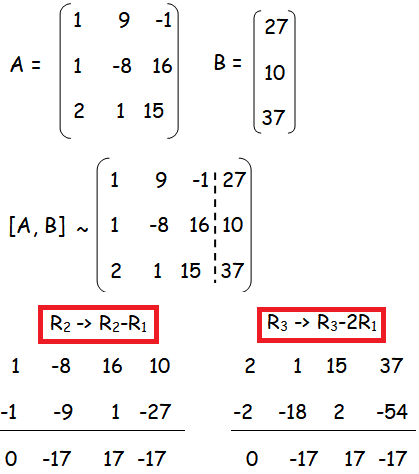
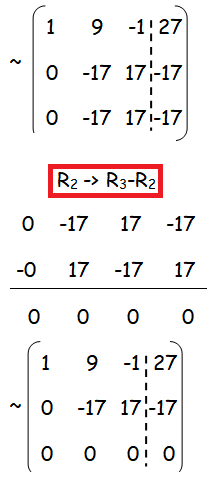
Here ρ(A) = ρ([A|B]) = 2 < 3, then the system is consistent and it has infinitely many solution.
From the 1st row,
x + 9y - z = 27 ---(1)
From the 2nd row,
17y + 17z = -17 ---(2)
Dividing by 17, we get
y + z = -1
Put z = t
y = -1 - t
By applying the value of y and z in (1), we get
x + 9(-1 - t) - t = 27
x - 9 + 9t - t = 27
x = 27 + 9 -8t
x = 36 - 8t
x = 36 - 8t, y = -1 - t and z = t where t ∈ Real numbers.
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com
Recent Articles
-
Quantitative Reasoning Questions and Answers
Dec 14, 25 06:42 AM
Quantitative Reasoning Questions and Answers -
Specifying Units of Measure
Dec 14, 25 06:38 AM
Specifying Units of Measure -
Coin Tossing Probability
Dec 13, 25 10:11 AM
Coin Tossing Probability - Concept - Sample Space - Formula - Solved Problems