RANGE IN STATISTICS

For a given set of observations, range may be defined as the difference between the largest and smallest of observations.

Thus if L and S denote the largest and smallest observations respectively then we have

Range  =  L - S

Coefficient of Range

The corresponding relative measure of dispersion, known as coefficient of range, is given by

For a grouped frequency distribution, range is defined as the difference between the two extreme class boundaries.

The corresponding relative measure of dispersion is given by the ratio of the difference between the two extreme class boundaries to the total of these class boundaries, expressed as a percentage.

Properties of Range

1)  Range remains unaffected due to a change of origin but affected in the same ratio due to a change in scale i.e., if for any two constants a and b, two variables x and y are related by y = a + bx,

Then the range of y is given by

Rᵧ  =  |b| x Rₓ

2)  It can be computed quickly.

3) The major application of range is statistical quality control.

4)  Range is based on only two observations and affected too much by the presence of extreme observation(s).

Solved Problems

Problem 1 : 

Following are the wages of 8 workers expressed in dollars :

82, 96, 52, 75, 70, 65, 50, 70.

Find the range and also it’s coefficient.

Solution :

The largest and the smallest wages are  L  =  96 and S  =  50

Thus,

Range  =  96 – 50  

Range  =  46

Coefficient of range  =  [ (96 - 50) / (96 + 50) ] x 100

Coefficient of range  =  31.51

Problem 2 : 

What is the range and its coefficient for the following distribution of weights ?

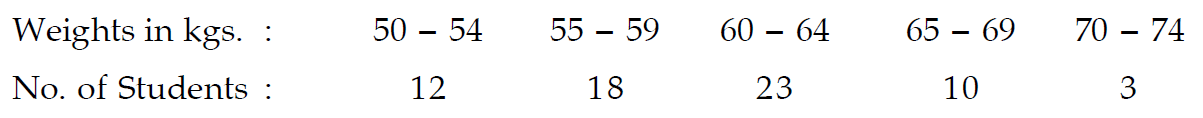
Solution :

The lowest class boundary is 49.50 kgs. and the highest class boundary is 74.50 kgs.

Thus we have

Range : 

=  74.50 – 49.50

=  25 kg

Coefficient of range : 

 =  [(74.50 - 49.50)/(74.50 + 49.50)] x 100

=  (25/124) x 100

=  20.16

Problem 3 : 

If the relationship between x and y is given by 2x+3y = 10 and the range of x is Rs. 15, what would be the range of y ?

Solution :

2x + 3y  =  10

Therefore,  y  =  (10/3) - 2x/3

For the given information, the range of 'y' is given by

Rᵧ  =  |b| x Rₓ

Rᵧ  =  |-2/3| x 15

Rᵧ  =  (2/3) x 15

Rᵧ  =  10

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.