PROPERTIES OF RADICALS
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
1. If two or more radicals are multiplied with the same index, you can take the radical once and multiply the numbers inside the radicals.
n√a x n√b = n√(a x b)
2. If two radicals are in division with the same index, you can take the radical once and divide the numbers inside the radicals.
n√a/n√b = n√(a/b)
3. One number can be taken out of a square root for every two same numbers multiplied inside the square root. And also, one number can be taken out of a cube root for every three same numbers multiplied inside the cube root and so on.
√4 = √(2 x 2) = 2
3√8 = 3√(2 x 2 x 2) = 2
4. A radical with index n can be written as exponent 1/n.
n√a = a1/n
√a = a1/2
3√a = a1/3
5. Addition and subtraction of two or more radicals can be performed with like radicals and like radicands only.
Like radicals - Radicals with the same index
Radicand - The number inside the radical
For example, 9√3 and 4√3 can be added or subtracted. Because the numbers inside the square roots are same.
9√3 + 4√3 = 13√3
9√3 - 4√3 = 5√3
6. If a radical with index n is moved from one side of the equation to the other side, it will become the exponent n.
n√x = a
x = an
7. If an exponent n is moved from one side of the equation to the other side, it will become a radical with index n.
yn = b
y = n√b
8. If the digit in one's place of a number is 2, 3, 7 or 8, then the number can not be a perfect square. So the square root of such numbers will be irrational.
For example, √23 = 4.795831.........
9. If a number ends with odd number of zeros, then, the square root of the number will be irrational.
For example, √3000 = 54.772255.......
10. The square root of a perfect square is always a rational number.
√4 = √(2 x 2) = 2
√25 = √(5 x 5) = 5
11. The square root of an even perfect square number is always even and the square root of an odd perfect square number is always is odd.
For example,
√64 = 8
√81 = 9
12. Square root of a negative number is considered to be an imaginary value.
For example, √(-2), √(-9).
Solved Problems
Problem 1 :
Simplify :
√6 ⋅ √15
Solution :
= √6 ⋅ √15
= √(6 ⋅ 15)
= √(2 ⋅ 3 ⋅ 3 ⋅ 5)
= 3√(2 ⋅ 5)
= 3√10
Problem 2 :
Simplify :
√35 ÷ √7
Solution :
= √35 ÷ √7
= √(35/7)
= √5
Problem 3 :
Simplify :
3√425 + 4√68
Solution :
Decompose 425 and 68 into prime factors using synthetic division.
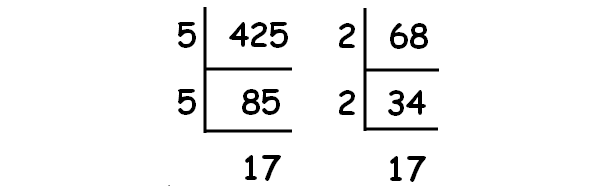
|
√425 = √(5 ⋅ 5 ⋅ 17) √425 = 5√17 |
√68 = √(2 ⋅ 2 ⋅ 17) √68 = 2√17 |
3√425 + 4√68 :
= 3(5√17) + 4(2√17)
= 15√17 + 8√17
= 23√17
Problem 4 :
Simplify :
√243 - 5√12 + √27
Solution :
Decompose 243, 12 and 27 into prime factors using synthetic division.
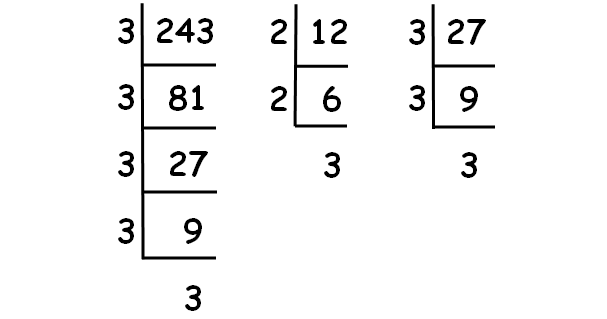
√243 = √(3 ⋅ 3 ⋅ 3 ⋅ 3 ⋅ 3) = 9√3
√12 = √(2 ⋅ 2 ⋅ 3) = 2√3
√27 = √(3 ⋅ 3 ⋅ 3) = 3√3
√243 - 5√12 + √27 :
= 9√3 - 5(2√3) + 3√3
= 9√3 - 10√3 + 3√3
= 2√3
Problem 5 :
Simplify :
√4 + 3√27 + 4√64
Solution :
√4 = √(2 ⋅ 2) = 2
3√27 = 3√(3 ⋅ 3 ⋅ 3) = 3
4√625 = 4√(5 ⋅ 5 ⋅ 5 ⋅ 5) = 5
√4 + 3√27 + + 4√64 :
= 2 + 3 + 5
= 10
Problem 6 :
Simplify :
3√4 ⋅ 3√16
Solution :
= 3√4 ⋅ 3√16
= 3√(4 ⋅ 16)
= 3√(4 ⋅ 4 ⋅ 4)
= 4
Problem 7 :
If 3√a = 1/2, then find the value of a.
Solution :
3√a = 1/2
a = (1/2)3
a = 13/23
a = 1/8
Problem 8 :
If (3√8)7 ⋅ (√2)-4 = 2k, then solve for k.
Solution :
(3√8)7 ⋅ (√2)-4 = 2k
27 ⋅ (21/2)-4 = 2k
27 ⋅ 2-2 = 2k
27 - 2 = 2k
25 = 2k
k = 5
Problem 9 :
The ratio of the length to the width of a golden rectangle is (1+√5) : 2. The dimensions of the face of the Parthenon in Greece form a golden rectangle. What is the height h of the Parthenon?

Solution :
(1 + √5) : 2 = 31 : h
(1 + √5) / 2 = 31 / h
Doing cross multiplication, we get
h = 2(31) / (1 + √5)
h = 62/(1 + √5)
Rationalizing the denominator, we get
h = [62/(1 + √5)] [(1 - √5)/(1 - √5)]
= 62(1 - √5) / (12 - √52)
= 62(1 - √5) / (1 - 5)
= 62(1 - √5) / (-4)
= -15.5(1 - 2.23)
= -15.5 + 34.56
= 19.06
So, the height is about 19 meters.
Problem 10 :
A sports teacher wants to arrange 6000 students in a field such that the number of rows is equal to number of columns. Find the number of rows if 71 were left out after arrangement.
Solution :
Total number of students = 6000
Number of students left = 6000 - 71
= 5929
Since the number of rows and number of columns should be filled with the same number of students, we have to find the square root of 5929.
√5929 = √(7 x 7 x 11 x 11)
= 7 x 11
= 77
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
10 Hard SAT Math Questions (Part - 38)
Dec 08, 25 12:12 AM
10 Hard SAT Math Questions (Part - 38) -
SAT Math Practice
Dec 05, 25 04:04 AM
SAT Math Practice - Different Topics - Concept - Formulas - Example problems with step by step explanation -
10 Hard SAT Math Questions (Part - 37)
Dec 03, 25 07:02 AM
10 Hard SAT Math Questions (Part - 37)


