RADIAN MEASURE OF AN ANGLE
For theoretical applications, the radian is the most common system of angle measurement. Radians are common unit of measurement in many technical fields, including calculus. The most important irrational number π plays a vital role in radian measures of angles.
Let us introduce the radian measure of an angle.
The radian measure of an angle is the ratio of the arc length it subtends, to the radius of the circle in which it is the central angle.
Consider a circle of radius r. Let s be the arc length subtending an angle θ at the center.
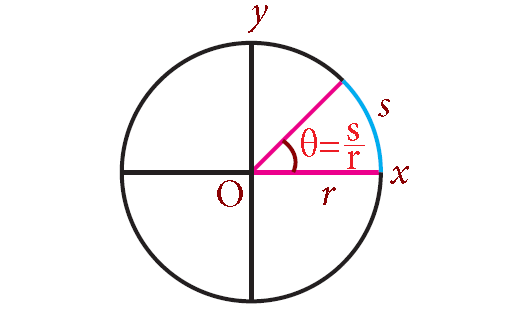
Then,
θ = arc length/radius = s/r radians
Hence,
s = rθ
Points to Remember
1. All circles are similar. Thus, for a given central angle in any circle, the ratio of the intercepted arc length to the radius is always constant.
2. When s = r, we have an angle of 1 radian. Thus, one radian is the angle made at the center of a circle by an arc with length equal to the radius of the circle.
3. Since the lengths s and r have same unit, θ is unitless and thus, we do not use any notation to denote radians.
4.
θ = 1 radian measure, if s = r
θ = 2 radian measure, if s = 2r
Thus, in general θ = k radian measure, if s = kr.
Hence, radian measure of an angle tells us how many radius lengths, we need to sweep out along the circle to subtend the angle θ.
5. Radian angle measurement can be related to the edge of the unit circle. In radian system, we measure an angle by measuring the distance travelled along the edge of the unit circle to where the terminal side of the angle intercepts the unit circle.
Problem 1 :
Convert each angle from degrees to radians, giving your answers in terms of π.
a) 180° b) 30° c) 45° d) 720° e) 18° f) 120°
Solution :
a) 180°
To convert degree measure to radian, we have to multiply by π/180
= 180 x (π/180)
= π
b) 30°
= 30 x (π/180)
= π/6
c) 45°
= 45 x (π/180)
= π/4
d) 720°
= 720 x (π/180)
= 72π/18
= 4π
e) 18°
= 18 x (π/180)
= 18π/180
= π/10
f) 120°
= 120 x (π/180)
= 12π/18
= 2π/3
Problem 2 :
Convert each angle from degrees to radians, giving your answers to 2 decimal places.
a) 63.8° b) 507° c) 126.2°
Solution :
a) 63.8°
= 63.8 x (π/180)
= 63.8(3.14)/180
= 200.332/180
= 1.11
b) 507°
= 507 x (π/180)
= 507(3.14)/180
= 1591.98/180
= 8.84
c) 126.2°
= 126.2° x (π/180)
= 126.2(3.14)/180
= 396.268/180
= 2.20
Problem 3 :
Convert each angle from radians to degrees.
a) 2π b) π/3 c) π/2 d) 3π/4
Solution :
a) 2π
To convert radian to degree measure, we have to multiply by 180/π
2π = 2π x (180/π)
= 360°
b) π/3
π/3 = π/3 x (180/π)
= 60°
c) π/2
π/2 = π/2 x (180/π)
= 90°
d) 3π/4
3π/4 = 3π/4 x (180/π)
= 3(45)
= 135°
Find, in terms of π, the length of the arc in each of the following circular sectors
Problem 4 :
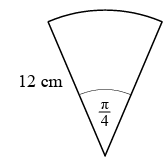
Solution :
Angle created is π/4
radius = 12 cm
Length of arc = rθ
= 12 (π/4)
= 3π
So, the lenght of arc is 3π radians.
Problem 5 :
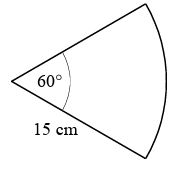
Solution :
Angle created is 60°
radius = 15 cm
Length of arc = (θ/360) x 2πr
= (60/360) x 2 x 3.14