QUOTIENTS AND PLACEMENT OF NEGATIVE SIGNS

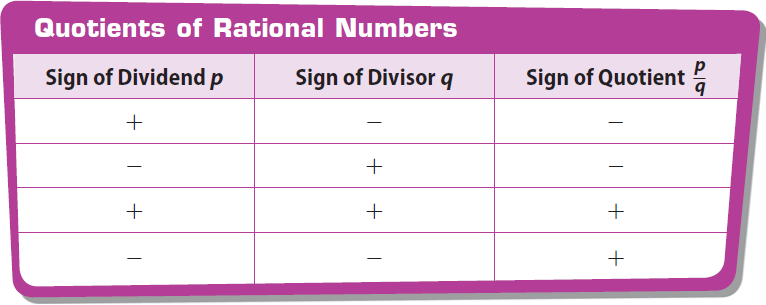
Quotients can have negative signs in different places.

When two two rational are divided, the rules for the sign of quotient are summarized below.

Let p and q be rational numbers.

Practice Questions

Question 1 : 

Are the rational numbers 12/(-4), (-12)/4 and -(12/4) equivalent ?

Answer : 

Find each quotient. Then use the rules in the table to make sure the sign of the quotient is correct.

12/(-4)  =  -3

(-12)/4  =  -3

-(12/4)  =  -3

Question 2 : 

What do you notice about each quotient ?

Answer : 

The quotients are all the same.

Question 3 : 

The rational numbers are / are not equivalent ?

Answer : 

The rational numbers are equivalent.

Question 4 : 

Explain how the placement of the negative sign in the rational number affects the sign of the quotients.

Answer : 

The sign of the quotient is not affected by the placement of the negative sign.

Question 5 : 

If p and q are rational numbers and q is not zero, what do you know about - (p/q) , -p/q, and p/(-q) ?

Answer : 

In all the rational numbers the dividend and divisor are same. Since the sign of the quotient is not affected by the placement of the negative sign, all the given rational numbers are equivalent. 

Question 6 : 

Write two equivalent quotients for the expression 14/(-7).

Answer : 

Since the sign of the quotient is not affected by the placement of the negative sign, we can take the negative sign at anywhere. 

The two equivalent quotients of 14/(-7) are

(-14)/7 and -(14/7) 

Question 7 : 

Write two equivalent quotients for the expression (-32)/(-8).

Answer : 

According to the rule given above, if both the dividend and divisor are negative, the quotient is always positive. 

The two equivalent quotients of (-32)/(-8) are

32/8 and -(-32/8) 

Question 8 : 

Find the quotient when we divide -36 by 9.

Answer : 

Find the quotient when 36 is divided by 9. 

36 / 9  =  4

According to the rule given above, if the dividend is negative and divisor is positive, the quotients is negative. 

So,

(-36)/9  =  -4

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.