QUOTIENT RELATION OF TRIGONOMETRIC RATIOS

Quotient Relation of Trigonometric Ratios

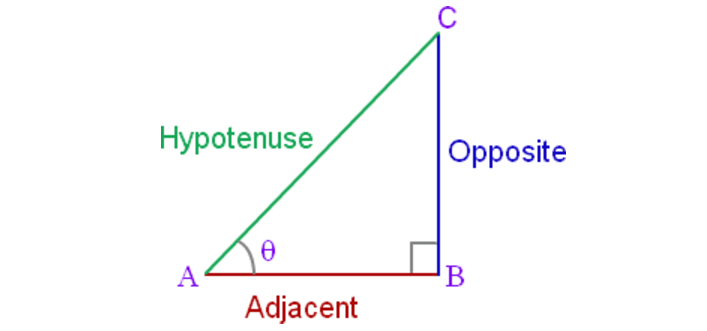
In the triangle above, according SOHCAHTOA, we have

sin θ  =  opposite side / hypotenuse  =  BC / AC

cos θ  =  adjacent side / hypotenuse  =  AB / AC

Now, let us divide sin θ by cos θ.

sin θ / cos θ  =  (BC/AC) ÷ (AB/AC)

sin θ / cos θ  =  (BC/AC) ⋅ (AC/AB)

sin θ / cos θ  =  BC /AB

  sin θ / cos θ  =  tan θ

(Because, tanθ = opposite side / adjacent side  =  BC / AB)

Therefore, 

sin θ / cos θ  =  tan θ

Now, let us divide cos θ by sin θ.

cos θ / sin θ  =  (AB/AC) ÷ (BC/AC)

cos θ / sin θ  =  (AB/AC) ⋅ (AC/BC)

cos θ / sin θ  =  AB / BC

cos θ / sin θ  =  cot θ

(Because, cotθ = adjacent side / opposite side  =  AB / BC)

Therefore, 

cos θ / sin θ  =  cot θ

csc θ  =  1 / sin θ  =  AC / BC

sec θ  =  1 / cos θ  =  AC / AB

Now, let us divide csc θ by sec θ.

csc θ / sec θ  =  (AC/BC) ÷ (AC/AB)

csc θ / sec θ  =  (AC/BC) ⋅ (AB/AC)

csc θ / sec θ  =  AB / BC

  csc θ / sec θ  =  cot θ

(Because, cotθ = adjacent side / opposite side  =  AB / BC)

Therefore, 

csc θ / sec θ  =  cot θ

Now, let us divide sec θ by csc θ.

sec θ / csc θ  =  (AC/AB) ÷ (AC/BC)

sec θ / csc θ  =  (AC/AB) ⋅ (BC/AC)

sec θ / csc θ  =  BC / AB

sec θ / csc θ  =  tan θ

(Because, tanθ = opposite side/adjacent side  =  BC / AB)

Therefore, 

sec θ / csc θ  =  tan θ

Practice Problems

Problem 1 :

In the right triangle PQR shown below, find the value of sin θ and cos θ. Using them, find the value of tan θ and cot θ.

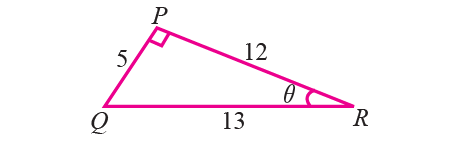
Solution :

From the right triangle shown above,

opposite side  =  5

adjacent side  =  12

hypotenuse  =  13

Therefore,

sin θ  =  PQ/RQ  =  5/13

cos θ  =  PR/RQ  =  12/13

tan θ  =  sin θ / cos θ  =  (5/13) ÷ (12/13)

tan θ  =  (5/13) ⋅ (13/12)

tan θ  =  5/12

cot θ  =  cos θ / sin θ  =  (12/13) ÷ (5/13)

cot θ  =  (12/13) ⋅ (13/5)

cot θ  =  12/5

Problem 2 :

From the figure given below, find the value of sin θ and cos θ. Using them, find the value of tan θ and cot θ.

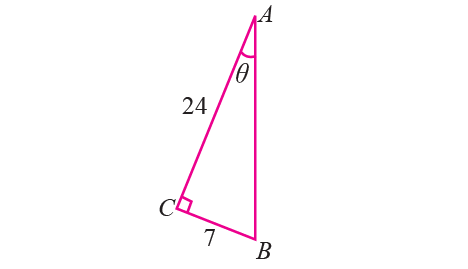
Solution : 

From the figure given above, AC = 24 and BC = 7.

By Pythagorean theorem, 

AB²  =  BC² + CA²

AB²  =  7² + 24²

AB²  =  49 + 576

AB²  =  49 + 576

AB²  =  625

AB²  =  25²

AB  =  25 

Now, we can use the three sides to find the six trigonometric ratios of angle θ.

Therefore, 

opposite side  =  7

adjacent side  =  24

hypotenuse  =  25

Therefore,

sin θ  =  BC/AB  =  7/25

cos θ  =  AC/AB  =  24/25

tan θ  =  sin θ / cos θ  =  (7/25) ÷ (24/25)

tan θ  =  (7/25) ⋅ (25/24)

tanθ  =  7/24

sin θ  =  BC/AB  =  7/25

cos θ  =  AC/AB  =  24/25

cot θ  =  cos θ / sin θ  =  (24/25) ÷ (7/25)

cot θ  =  (24/25) ⋅ (25/7)

cot θ  =  24/7

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.