QUESTIONS ON LINEAR FUNCTIONS

Question 1 :

Let f = {(-1, 3), (0, -1), (2, -9)} be a linear function from Z into Z . Find f(x).

Answer :

Let the linear function be f(x) = ax + b. 

From the ordered pair (-1, 3), x = -1, f(x) = 3.

3 = a(-1) + b

3 = -a + b ----(1)

From the ordered pair (0, -1), x = 0, f(x) = -1.

-1 = a(0) + b

-1 = b

Substitute b = -1 in (1). 

3 = -a + (-1)

3 = -a - 1

Add a to each side. 

3 + a = -1

Subtract 3 from each side. 

a = -4

So, the linear function is f(x) = -4x - 1.

Question 2 :

In electrical circuit theory, a circuit C(t) is called a linear circuit if it satisfies the superposition principle given by C(at₁ + bt₂) = aC(t₁) + bC(t₂), where a, b are constants. Show that the circuit C(t) = 3t is linear.

Answer :

Take two points t₁ and t₂ from domain of C(t).

C(at₁) =  aC(t₁)

C(at₂) =  aC(t₂)

It is given that C(t) = 3t.

C(t) = 3t

C(at₁ + bt₂)  =  3(at₁ + at₂)

C(at₁ + bt₂)  =  3at₁ + 3at₂

C(at₁ + bt₂)  =  a(3t₁) + a(3t₂)

C(at₁ + bt₂)  =  aC(t₁) + aC(t₂)

Superposition principle is satisfied. 

Hence c(t) = 3t is linear. 

Question 3 :

The cost of a school banquet is $95 plus $15 for each person attending. Write a linear function that gives total cost of the number of people attending. What is the cost for 77 people?

Solution :

Let f(x) be the total cost and x be the number of persons attending the banquet.

Linear function that gives total cost :

f(x) = 95 + 15x

To find the cost for 77 people, substitute x = 77. 

f(77) = 95 + 15(77)

= 95 + 1155

= 1250

So, the total cost of attending 77 people is $1250.

Question 4 :

A manufacturer produces 80 units of a particular product at a cost of $ 220000 and 125 units at a cost of $ 287500. Assuming the cost curve to be linear, find the cost of 95 units. 

Solution :

Because the cost curve is linear, the function which best fits the given information will be a linear-cost function.

y = Ax + B

y ----> Total cost

x ----> Number of units

Target : To find the value of y when x = 95.

From the question, we have

x = 80 and y = 220000

x = 75 and y = 287500

Substitute the above values for x and y in 'y = Ax + B'. 

220000 = 80A + B

287500 = 75A + B

Solve for x and y. 

A = 1500 and B = 100000

The linear cost function :   

y = 1500x + 100000

Substitute x = 95. 

y = 1500x + 100000

y = 1500x95 + 100000

y = 142500  +  100000

y = 242500

So, the cost of 95 units is $242500.

Question 5 :

The number c of cartoons a cartoonist plans to complete by the nth day of the month is given by c = 24 + 4n. What does the y-intercept represent?

Solution :

c = 24 + 4n

Comparing the given equation with y = mx + b

c = 4n + 24

Here slope (m) = 4 and y-intercept is 24.

He started with 24 cartoons.

Question 6 :

The graph relates temperatures y (in degrees Fahrenheit) to temperatures x (in degrees Celsius).

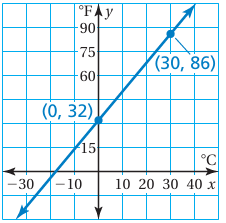
(a) Find the slope and y-intercept.

(b) Write an equation of the line.

(c) What is the mean temperature of Earth in degrees Fahrenheit?

Solution :

a) The points on the line are (0, 32) and (30, 86)

Slope = (86 - 32) / (30  -0)

= 54 / 30

= 27 /15

= 9/5

By observing the graph, the line is intersecting the y-axis at the point 32.

b)

Equation of the line :

y = mx + b

y = (9/5) x + 32

c) When x = 15

y = (9/5) (15) + 32

= 9(3) + 32

= 27 + 32

= 59

So, the mean temperature of the earth is 59 degree Fahrenheit.

Question 7 :

The graph shows the height y (in feet) of a flag x seconds after you start raising it up a flagpole.

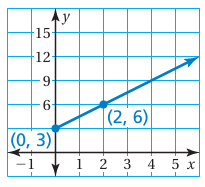
a. Find and interpret the slope.

b. Write an equation of the line.

c. What is the height of the fl ag after 9 seconds?

Solution :

a) Tracing two points on the line, they are (0, 3) and (2, 6).

Slope (m) = (6 - 3) / (2 - 0)

= 3/2

The line is intersecting the y-axis at the point 3. so, yu-intercept is 3.

b)  y = mx + b

y = (3/2)x + 3

c) After 9 seconds

Then x = 9

y = (3/2)(9) + 3

y = 27/2 + 3

y = 13.5 + 3

= 16.5

So, after 9 seconds the height of the flag is 16.5 feet.

Question 8 :

The graph shows the distance remaining to complete a tunnel.

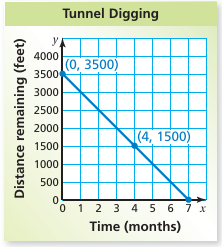
(a) Write an equation that represents the distance y (in feet) remaining after x months.

(b) How much time does it take to complete the tunnel?

Solution :

a) Points on the line (0, 3500) and (4, 1500)

Slope = (1500 - 3500) / (4 - 0)

= -2000 / 4

= -500

The y-intercept is 3500.

y = -500 x + 3500

b)  The tunnel is complete when the distance remaining is 0 feet. So, find the value of x when y = 0.

y = −500x + 3500

0 = −500x + 3500

500x = 3500

x = 3500/500

x = 7

It takes 7 months to complete the tunnel.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.