QUESTIONS ON FUNDAMENTAL THEOREM OF ARITHMETIC

Question 1 :

For what values of natural number n, 4ⁿ can end  with the digit 6?

Solution :

4ⁿ

if n = 1, then 4¹  =  4

if n = 2, then 4²  =  16

if n = 3, then 4³  =  64

if n = 4, then 4⁴  =  256

if n = 5, then 4⁵  =  1024

if n = 6, then 4⁶  =  4096

When n is even, 4ⁿ ends with 6.

Question 2 :

If m, n are natural numbers, for what values of m, does 2ⁿ x 5^m ends in 5?

Solution :

For any value of n, 2ⁿ will become even.

For any value m, 5^m ends with 5. The product of even number and a number ends with the digit 5, we get the answer ends with 0.

We should not apply the value 0 for n and m, because n and m are natural numbers.

Question 3 :

Find the HCF of 252525 and 363636.

Solution :

252525  =  5²⋅ 3 ⋅ 7 ⋅ 13 ⋅ 37

363636  =  2²⋅ 3³ ⋅ 7 ⋅ 13 ⋅ 37

H.C.F  =  3 ⋅ 7 ⋅ 13 ⋅ 37   =  10101

Question 4 :

If 13824 = 2^a ×3^b then find a and b.

Solution :

To find the values of a and b, we have decompose 13824 as the product of prime factors.

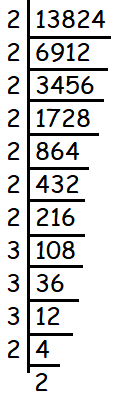
13824 =  2⁹ x 3³

Hence the value of a is 9 and b is 3.

Question 5 :

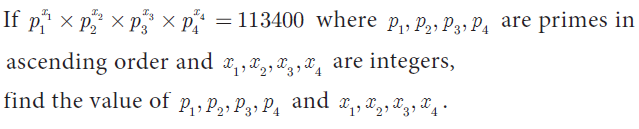
Solution :

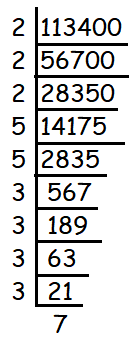
113400  =  2³ x 3⁴ x 5² x 7¹

The values of p₁, p₂, p₃ and p₄ are 2, 3, 5 and 7 respectively.

The values of x₁, x₂, x₃ and x₄ are 3, 4, 2 and 1 respectively.

Question 6 :

Find the LCM and HCF of 408 and 170 by applying the fundamental theorem of arithmetic.

Solution :

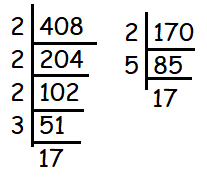
408  =  2³ x 3 x 17

170  =  2 x 5 x 17

Common factors are 2 and 17 

H.C.F  =  34

L.C.M  =  2³ x 3 x 5 x 17

L.C.M  =  2040

Question 7 :

Find the greatest number consisting of 6 digits which is exactly divisible by 24,15,36?

Solution :

We will find out the LCM of 24,15 and 36 is 360.

The greatest 6-digit number is 999999.

Now, We will divide this number by LCM of 24,15 and 36, we will get,

999999/360 will get remainder 279.

Now 999999 – 279 = 999720.

Now we will check it out for the numbers we will get,

999720/24 = 41655

999720/15 = 66648

999720/36 = 27770

999720 is the greatest number 6-digit number divisible by 24,15 and 36.

Question 8 :

What is the smallest number that when divided by three numbers such as 35, 56 and 91 leaves remainder 7 in each case?

Solution :

The smallest number which when divided by 35, 56 and 91 = LCM of 35, 56 and 91

35 = 5 x 7

56 = 2 x 2 x 2 x 7

91 = 7 x 13

LCM = 7 x 5 x 2 x 2 x 2 x 13 = 3640

The smallest number that when divided by 35, 56, 91 leaves a remainder 7 in each case = 3640 + 7 = 3647.

Question 9 :

Find the least number that is divisible by the first ten natural numbers.

Solution :

first 10 natural numbers:

                    1, 2, 3, 4, 5, 6, 7, 8, 9, 10

L.C.M of these natural numbers:

Factors = 2 × 2 × 2 × 3 × 3 × 5 × 7

  =  2520

The smallest number is 2520.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.