QUADRILATERAL PRACTICE PROBLEMS FOR 9TH GRADE

Question 1 :

Show that the bisectors of angles of a parallelogram form a rectangle .

Solution :

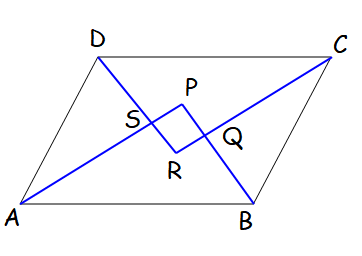
In triangle ADS,

<SAD  =  (1/2)<A   ----(1)

<ADS  =  (1/2) <D   ----(2)

(1) + (2)

<SAD + <ADS  =  (1/2) [<A + <D]

<SAD + <ADS  =  (1/2) (180)

<SAD + <ADS  =  90

 In triangle ADS,

<SAD + <ASD + <SDA  =  180

<SAD + <SDA + <ASD  =  180

90 + <ASD  =  180

<ASD  =  180 - 90

<ASD  =  90, <PSR  =  90 (Vertically opposite angle)

Hence PQRS is a rectangle.

Question 2 :

If a triangle and a parallelogram lie on the same base and between the same parallels, then prove that the area of the triangle is equal to half of the area of parallelogram.

Solution :

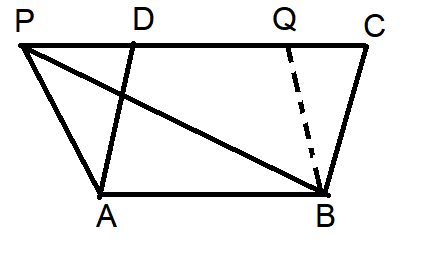
Let ΔABP and a parallelogram ABCD be on the same base AB and between the same parallels AB and PC.

To Prove : ar( ΔPAB ) = (1/2)ar( ABCD)

Draw BQ ||AP to obtain another parallelogram.ABQP and ABCD are on the same base AB and between the same parallels AB and PC.

Therefore, ar(ABQP) =  ar(ABCD)

But ΔPAB ≅ ΔBQP( Diagonals PB divides parallelogram ABQP into two congruent triangles.

So  ar (PAB) = ar(BQP) -----------(2)

ar (PAB) = (1/2)ar(ABQP) -----------------(3)

This gives ar (PAB) = (1/2)ar(ABCD)

Question 3 :

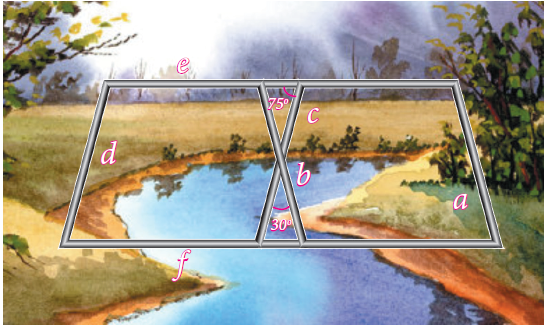
Iron rods a, b, c, d, e, and f are making a design in a bridge as shown in the figure. If a || b , c || d , e || f , find the marked angles between

(i) b and c

(ii) d and e

(iii d and f

(iv) c and f

Solution :

(i)  Angle between b and c is 30.

(ii)  Angle  between d and e :

75 + angle between d and e  =  180

Angle between d and e  =  180 - 75

  =  105

(iii)  Angle between d and f :

In a parallelogram opposite angles will be equal.

Angle between d and is also 75.

(iv)  Angle between c and f :

In a parallelogram opposite angles will be equal.

Angle between c and f is 105.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.