QUADRATICS WORD PROBLEMS WITH ANSWERS

To see from questions 1 to 3, please visit the page "Solving Word Problems Involving Quadratic Equations"

Question 4 :

A girl is twice as old as her sister. Five years hence, the product of their ages (in years) will be 375. Find their present ages.

Solution :

Let "x" be the age of sister

"2x" be the age of girl

Five years hence,

age of sister  =  x + 5

Age of girl  =  2x + 5

Product of their ages  =  375

(x + 5)(2x + 5 )  =  375

2x² + 5x + 10x + 25 - 375  =  0

2x² + 15x - 350  =  0

2x² - 20x + 35x - 350  =  0

2x(x - 10) + 35(x -10)  =  0

(2x + 35)(x - 10)  =  0

 x = 10

Hence the age of sister is 10 years, age of girl  =  2(10)  =  20 years.

Question 5 :

A pole has to be erected at a point on the boundary of a circular ground of diameter 20 m in such a way that the difference of its distances from two diametrically opposite fixed gates P and Q on the boundary is 4 m. Is it possible to do so? If answer is yes at what distance from the two gates should the pole be erected?

Solution :

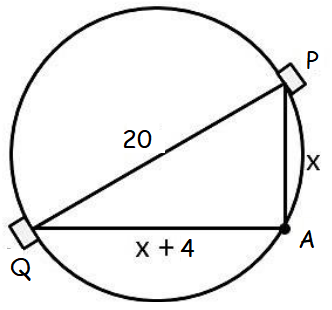
x² + (x + 4)²  =  20²

x² + x² + 2x(4) + 4²  =  400

2x² + 8x + 16 - 400  =  0

2x² + 8x - 384  =  0

x² + 4x - 192  =  0

(x + 16)(x- 12)  =  0

x + 16  =  0  and x - 12  =  0

x  =  -16 and x = 12.

Hence  required distance is 12 m and 16 m.

Question 6 :

From a group of 2x² black bees , square root of half of the group went to a tree. Again eight-ninth of the bees went to the same tree. The remaining two got caught up in a fragrant lotus. How many bees were there in total?

Solution :

Total number of bees  =  2x²

Number of bees went to tree  =  (1/2)√x²  =  x

Number of bees went to the same tree  =  (8/9)2x^{2  =}  16x²/9

Remaining number of bees  =  2

x + (16x²/9) + 2  =  2x² 

9x + 16x² + 18  =  18x²

18x²- 16x² - 9x - 18  =  0

2x² - 9x - 18  =  0

2x² - 12x + 3x - 18  =  0

2x(x - 6) + 3(x - 6)  =  0

(2x + 3)(x -  6)  =  0

x - 6  =  0, 2x + 3  =  0

x  =  6, x = -3/2 (not possible)

Total number of bees  =  2(6)²  =  2(36)  =  72

Hence total number of bees  =  72.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.