QUADRATIC EQUATIONS WORKSHEET
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Problem 1 :
Solve the following quadratic equation by factoring.
x2 – 5x – 24 = 0
Problem 2 :
If one root of a quadratic equation (2 + √3), then form the equation given that the roots are irrational.
Problem 3 :
If α and β be the roots of x2 + 7x + 12 = 0, find the quadratic equation whose roots are
(α + β)2 and (α - β)2
Problem 4 :
A piece of iron rod costs $60. If the rod was 2 meter shorter and each meter costs $1 more, the cost would remain unchanged. What is the length of the rod?
Problem 5 :
Find the value :
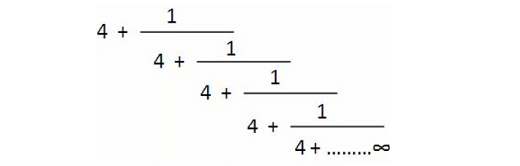
Problem 6 :
Solve for x in the following equation :
4x - 3 ⋅ 2x+2 + 25 = 0
Problem 7 :
If the sum of the roots of the quadratic equation
ax2 + bx + c = 0
is equal to the sum of the squares of their reciprocals, then find the value of
(b2/ac) + (bc/a2)
Problem 8 :
If L + M + N = 0 and L, M, N are rationales, examine the nature of the roots of the equation
(M + N - L)x2 + (N + L - M)x + (L + M - N) = 0
Problem 9 :
If p ≠ q and p2 = 5p - 6, q2 = 5q - 6, find the quadratic equation having roots p/q and q/p.
Problem 10 :
If one root of the equation x2 - 8x + m = 0 exceeds the other by 4, then find the value of m.

1. Solution :
x2 – 5x – 24 = 0
In the given quadratic equation, the coefficient of x2 is 1.
Decompose the constant term -24 into two factors such that the product of the two factors is equal to -24 and the addition of two factors is equal to the coefficient of x, that is 5.
Then, the two factors of -24 are
+3 and -8
Factor the given quadratic equation using +3 and -8 and solve for x.
(x + 3)(x - 8) = 0
x + 3 = 0 or x - 8 = 0
x = -3 or x = 8
So, the solution is {-3, 8}.
2. Solution :
(2 + √3) is an irrational number.
We already know the fact that irrational roots of a quadratic equation will occur in conjugate pairs.
That is, if (2 + √3) is one root of a quadratic equation, then (2 - √3) will be the other root of the same equation.
So, (2 + √3) and (2 - √3) are the roots of the required quadratic equation.
Sum of the roots is
= (2 + √3) + (2 - √3)
= 4
Product of the roots is
= (2 + √3)(2 - √3)
= 22 - √32
= 4 - 3
= 1
Formation of quadratic equation :
x2 - (sum of the roots)x + product of the roots = 0
x2 - 4x + 1 = 0
3. Answer :
Given : α and β are the roots of x2 + 7x + 12 = 0.
sum of roots = -coefficient of x/coefficient of x2
α + β = -7/1
α + β = -7
product of roots = constant term/coefficient of x2
αβ = 12/1
αβ = 12
Quadratic equation with roots (α + β)2 and (α - β)2 :
x2 - [(α + β)2 + (α - β)2]x + (α + β)2(α - β)2 = 0 ----(1)
Find the values of (α + β)2 and (α - β)2.
(α + β)2 = (-7)2
(α + β)2 = 49
(α - β)2 = (α + β)2 - 4αβ
(α - β)2 = (-7)2 - 4(12)
(α - β)2 = 49 - 48
(α - β)2 = 1
So, the required quadratic equation is
(1)-----> x2 - [49 + 1]x + 49 ⋅ 1 = 0
x2 - 50x + 49 = 0
4. Solution :
Let 'x' be the length of the given rod.
Then the length of the rod 2 meter shorter is (x - 2) and the total cost of both the rods is $60 (Because cost would remain unchanged).
Cost of one meter of the given rod is
= 60/x
Cost of one meter of the rod which is 2 meter shorter is
= 60/(x - 2)
Given : If the rod was 2 meter shorter and each meter costs $1 more.
That is, 60/(x - 2) is $1 more than 60/x.
[60/(x - 2)] - [60/x] = 1
Simplify.
[60x - 60(x - 2)]/[x(x - 2)] = 1
[60x - 60x + 120]/[x2 - 2x] = 1
120/(x2 - 2x) = 1
120 = x2 - 2x
x2 + 2x - 120 = 0
(x + 10)(x - 12) = 0
x = -10 or x = 12
Because length can not be a negative number, we can ignore - 10.
So, the length of the given rod is 12 m.
5. Solution :
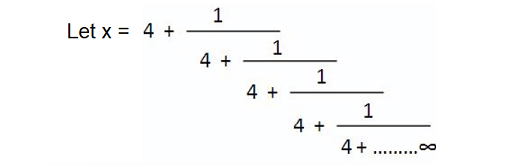
In this question, wherever you find the pattern shown below, it can be replaced by x.
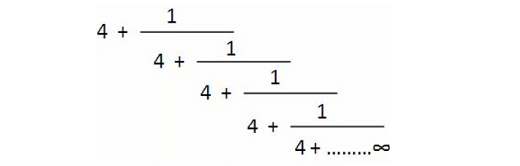
Then,
The quadratic equation above can not be solved by factoring. So, we can use quadratic formula and solve.
Comparing ax2 + bx + c = 0 and x2 - 4x - 1 = 0,
a = 1, b = -4 and c = -1
Quadratic formula :
Substitute a = 1, b = -4 and c = -1.
When we look at the given numerical expression, it is clear that its value must be greater than 4.
Therefore the value of the given numerical expression is
2 + √5
6. Solution :
4x - 3 ⋅ 2x+2 + 25 = 0
(2x)2 - 3 ⋅ 2x ⋅ 22 + 32 = 0
(2x)2 - 3 ⋅ 2x ⋅ 4 + 32 = 0
(2x)2 - 12 ⋅ 2x + 32 = 0
Let y = 2x.
y2 - 12y + 32 = 0
(y - 8)(y - 4) = 0
y - 8 = 0 or y - 4 = 0
y = 8 or y = 4
Replace y by 2x.
2x = 8 or 2x = 4
2x = 23 or 2x = 22
x = 3 or x = 2
So, the values of x are 3 and 2.
7. Solution :
Let 'α' and 'β' be the roots of the equation
ax2 + bx + c = 0
Given : Sum of the roots is equal to the sum of the squares of their reciprocals .
α + β = (1/α)2 + (1/β)2
α + β = 1/α2 + 1/β2
α + β = (α2 + β2)/(α2β2)
α + β = [(α + β)2 - 2αβ]/(αβ)2 ----(1)
In the quadratic equation ax2 + bx + c = 0,
sum of the roots = -b/a
product of the roots = c/a
α + β = -b/a
αβ = c/a
(1)----> -b/a = [(-b/a)2 - 2c/a]/(c/a)2
(-b/a) ⋅ (c2/a2) = b2/a2 - 2c/a
-bc2/a3 = b2/a2 - 2ac/a2
-bc2/a3 = (b2 - 2ac)/a2
-bc2 = a3 ⋅ [(b2 - 2ac)/a2]
-bc2 = a(b2 - 2ac)
-bc2 = ab2 - 2a2c
2a2c = ab2 + bc2
Divide both sides by a2c.
2 = b2/ac + bc/a2
So, the value of (b2/ac) + (bc/a2) is 2.
8. Solution :
Given : L + M + N = 0.
L + M = -N
M + N = -L
N + L = -M
Given : (M + N - L)x2 + (N + L - M)x + (L + M - N) = 0.
(-L - L)x2 + (-M - M)x + (-N - N) = 0
- 2Lx2 - 2Mx - 2N = 0
Divide both sides by -2.
Lx2 + Mx + N = 0
In the above quadratic equation a = L, b = M and c = N.
Substitute a = L, b = M and c = N in the discriminant of the quadratic equation (b2- 4ac).
b2- 4ac = M2 - 4LN
b2- 4ac = (-M)2 - 4LN
Substitute -M = L + N.
b2- 4ac = (L + N)2 - 4LN
b2- 4ac = L2 + N 2 + 2LN - 4LN
b2- 4ac = L2 + N 2 - 2LN
b2- 4ac = (L - N)2
Because b2-4ac > 0 and also a perfect square, the roots are real and rational.
9. Solution :
Given : p2 = 5p - 6 and q2 = 5q - 6.
p2 - 5p + 6 = 0 and q2 - 5q + 6 = 0
By solving the above quadratic equations, we get
p = -2, -3
q = -2, -3
Because p ≠ q, we can take p = -2 and q = -3.
p/q = -2/(-3) = 2/3
q/p = 3/2
Construction of quadratic equation :
x2 - (sum of the roots)x + product of the roots = 0
Quadratic equation having roots p/q and q/p :
x2 - (p/q + q/p)x + p/q ⋅ q/p = 0
x2 - (p/q + q/p)x + 1 = 0
Substitute p/q = 3/2 and q/p = 2/3.
x2 - (3/2 + 2/3)x + 1 = 0
x2 - (13/6)x + 1 = 0
Multiply both sides by 6.
6x2 - 13x + 6 = 0
Hence, the required quadratic equation is
6x2 - 13x + 6 = 0
10. Solution :
In the given equation x2 - 8x + m = 0, constant term m is positive.
The two factors of m must satisfy the following two conditions.
(i) Sum of the two factors of m must be equal to the middle term - 8.
(ii) One root of the equation must exceed the other by 4. That is, there must be a difference of 4 between the two roots.
The above two conditions can be met, only if the two factors of m are
- 2 and - 6
Then, we have
m = (- 2) ⋅ (- 6)
m = 12
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
Times Table Shortcuts
Dec 30, 25 07:14 PM
Times Table Shortcuts - Concept - Examples -
10 Hard SAT Math Questions (Part - 42)
Dec 30, 25 05:52 AM
10 Hard SAT Math Questions (Part - 42) -
10 Hard SAT Math Questions (Part - 38)
Dec 29, 25 04:21 AM
10 Hard SAT Math Questions (Part - 38)

