QUADRATIC EQUATION WORD PROBLEMS WORKSHEET WITH ANSWERS
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Problem 1 :
Difference between a number and its positive square root is 12. Find the number.
Problem 2 :
If the difference between a number and its reciprocal is ²⁴⁄₅, find the number.
Problem 3 :
A piece of iron rod costs $60. If the rod was 2 meter shorter and each meter costs $1 more, the cost would remain unchanged. What is the length of the rod?
Problem 4 :
Divide 25 in two parts so that sum of their reciprocals is ⅙.
Problem 5 :
The hypotenuse of a right angled triangle is 20 cm. The difference between its other two sides is 4 cm. Find the length of the sides.
Problem 6 :
The altitude of a right triangle is 7 cm less than its base. If the hypotenuse is 13 cm, find the other two sides.
Problem 7 :
A cottage industry produces a certain number of pottery articles in a day. It was observed on a particular day that the cost of production of each article(in dollars) was 3 more than twice the number of articles produced on that day. If the total cost of production on that day was $90, find the number of articles produced and the cost of each article.
Problem 8 :
The sides of an equilateral triangle are shortened by 12 units, 13 units and 14 units respectively and a right angle triangle is formed. Find the length of each side of the equilateral triangle.

Answers
1. Answer :
Let x be the required number.
Its positive square root is √x.
Given : Difference between x and √x is 12.
x - √x = 12
x - 12 = √x
(x - 12)2 = x
x2 - 24x + 144 = x
Subtract x from both sides.
x2 - 25x + 144 = 0
x2 - 9x - 16x + 144 = 0
x(x - 9) - 16(x - 9) = 0
(x - 9)(x - 16) = 0
x = 9 or x = 16
|
9 - √9 = 9 - 3 = 6 ≠ 12 |
16 - √16 = 16 - 4 = 12 |
x = 9 does not satisfy the condition given in the question.
Then,
x = 16
Therefore, the required number is 16.
2. Answer :
Let y be the required number.
Then, its reciprocal is ¹⁄y.
Given : Difference between a number and its reciprocal is ²⁴⁄₅.
y - ¹⁄y = ²⁴⁄₅
Multiply both sides by 5y to get rid of the denominators y and 5.
5y(y - ¹⁄y) = 5y(²⁴⁄₅)
5y(y) - 5y(¹⁄y) = 24y
5y2 - 5 = 24y
Subtract 24y from boths sides.
5y2 - 24y - 5 = 0
Solve by factoring.
5y2 - 25y + y - 5 = 0
5y(y - 5) + 1(y - 5) = 0
(y - 5)(5y + 1) = 0
y - 5 = 0 or 5y + 1 = 0
y = 5 or y = ⁻¹⁄₅
Justification :
|
5 - ⅕ = ²⁵⁄₅ - ⅕ = ⁽²⁵ ⁻ ¹⁾⁄₅ = ²⁴⁄₅ |
⁻¹⁄₅ - (-5) = ⁻¹⁄₅ + 5 = ⁻¹⁄₅ + ²⁵⁄₅ = ⁽⁻¹ ⁺ ²⁵⁾⁄₅ = ²⁴⁄₅ |
Both the values y = 5 and y = ⁻¹⁄₅ satisfy the condition given in the question.
Therefore, the required number is 5 or ⁻¹⁄₅.
3. Answer :
Let x be the length of the given rod.
Then the length of the rod 2 meter shorter is (x - 2) and the total cost of both the rods is $60 (Because cost would remain unchanged).
Cost of one meter of the given rod is
= ⁶⁰⁄ₓ
Cost of one meter of the rod which is 2 meter shorter is
= ⁶⁰⁄₍ₓ ₋ ₂₎
Given : If the rod was 2 meter shorter and each meter costs $1 more.
That is, 60/(x-2) is $1 more than 60/x.
⁶⁰⁄₍ₓ ₋ ₂₎ - ⁶⁰⁄ₓ = 1
Multiply both sides by x(x - 2) to get rid of the denominators (x - 2) an x.
x(x - 2)[⁶⁰⁄₍ₓ ₋ ₂₎ - ⁶⁰⁄ₓ] = x(x - 2)
x(x - 2)[⁶⁰⁄₍ₓ ₋ ₂₎] - x(x - 2)[⁶⁰⁄ₓ] = x(x - 2)
60x - 60(x - 2) = x2 - 2x
60x - 60x + 120 = x2 - 2x
120 = x2 - 2x
0 = x2 - 2x - 120
x2 - 2x - 120 = 0
Solve by factoring.
x2 - 12x + 10x - 120 = 0
x(x - 12) + 10(x - 12) = 0
(x - 12)(x + 10) = 0
x - 12 = 0 or x + 10 = 0
x = 12 or x = -10
Because length can not be a negative number, we can ignore x = -10.
Therefore, the length of the given rod is 12 m.
4. Answer :
Let x be one of the parts of 25.
Then, the other part is (25 - x).
Given : Sum of the reciprocals of the parts is 1/6.
¹⁄ₓ + ¹⁄₍₂₅ ₋ ₓ₎ = ⅙
Multiply both sides by 6x(25 - x) to get rid of the denominators x, (25 - x) and 6.
6x(25 - x)[¹⁄ₓ + ¹⁄₍₂₅ ₋ ₓ₎] = 6x(25 - x)[⅙]
6x(25 - x)[¹⁄ₓ] - 6x(25 - x)[¹⁄₍₂₅ ₋ ₓ₎] = x(25 - x)
6(25 - x) - 6x = 25x - x2
150 - 6x + 6x = 25x - x2
150 = 25x - x2
x2 - 25x + 150 = 0
Solve by factoring.
x2 - 15x - 10x + 150 = 0
x(x - 15) - 10(x - 15) = 0
(x - 15)(x - 10) = 0
x - 15 = 0 or x - 10 = 0
x = 15 or x = 10
When x = 15,
25 - x = 25 - 15
= 10
When x = 10,
25 - x = 25 - 10
= 15
Therefore, the two parts of 25 are 10 and 15.
5. Answer :
From the given information. we can assume x and (x + 4) as the lengths of the other two sides of the right triangle.
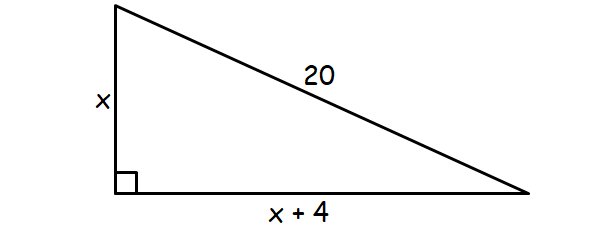
Using Pythagorean Theorem in the right triangle above,
x2 + (x + 4)2 = 202
x2 + (x + 4)(x + 4) = 400
x2 + x2 + 4x + 4x + 16 = 400
2x2 + 8x + 16 = 400
2x2 + 8x - 384 = 0
Divide both sides by 2.
x2 + 4x - 192 = 0
Solve by factoring.
x2 - 12x + 16x - 192 = 0
x(x - 12) + 16(x - 12) = 0
(x - 12)(x + 16) = 0
x - 12 = 0 or x + 16 = 0
x - 12 = 0 or x + 16 = 0
x = 12 or x = -16
x = -16 can not be accepted. Because length can never be negative.
So,
x = 12
x + 4 = 16
Therefore, the other two sides of the triangle are 12 cm and 16 cm.
6. Answer :
Let x be the base the right triangle.
Then, its altitude is (x - 7).
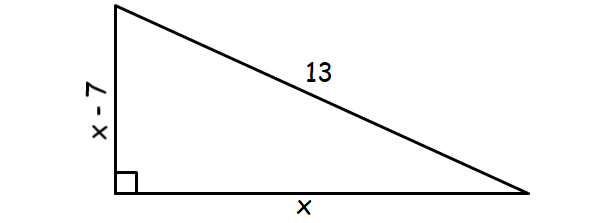
Using Pythagorean Theorem in the right triangle above,
x2 + (x - 7)2 = 132
x2 + (x - 7)(x - 7) = 169
x2 + x2 - 7x - 7x + 49 = 169
2x2 - 14x + 49 = 169
2x2 - 14x - 120 = 0
Divide both sides by 2.
x2 - 7x - 60 = 0
Solve by factoring.
x2 - 12x + 5x - 60 = 0
x(x - 12) + 5(x - 12) = 0
(x + 5)(x - 12) = 0
x + 5 = 0 or x - 12 = 0
x = -5 or x = 12
Because x represents the base of the triangle, it can never be negative. So, x = 12
Base = 12 cm
Altitude = 5 cm
Therefore, the other two sides of the right triangle are 12 cm and 5 cm.
7. Answer :
Let x be the number of articles produced on that day.
Then, the cost of production of each article is
= 2x + 3
Total cost = Number of articles ⋅ cost of one article
90 = x(2x + 3)
90 = 2x2 + 3x
2x2 + 3x - 90 = 0
Solv by factoring.
2x2 - 12x + 15 x - 90 = 0
2x(x - 6) + 15(x - 6) = 0
(2x + 15)(x - 6) = 0
2x + 15 = 0 or x - 6 = 0
x = -7.5 or x = 6
Because x represents the number of articles, it can never be negative value. Then, x = 6.
So, the number of articles produced is 6.
The cost of each article :
= 2x + 3
= 2(6) + 3
= 12 + 3
= $15
8. Answer :
Let x be the length of each side of the equilateral triangle.
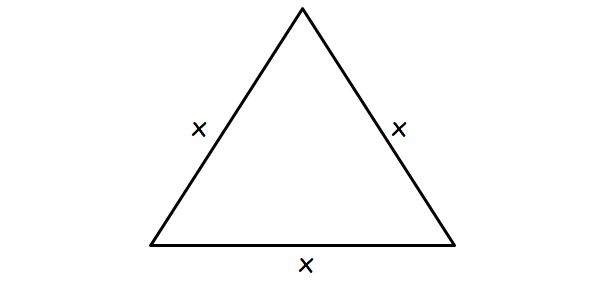
Then, the sides of the right angle triangle are
(x - 12), (x - 13) and (x - 14)
In the above three sides, the side represented by (x - 12) is hypotenuse (because, that is the longest side).
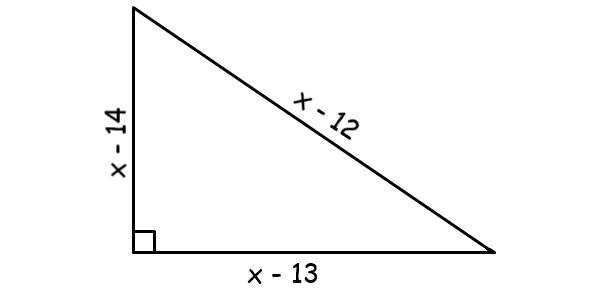
Using Pythagorean Theorem in the right triangle above,
(x - 13)2 + (x - 14)2 = (x - 12)2
(x - 13)(x - 13) + (x - 14)(x - 14) = (x - 12)(x - 12)
x2 - 26x + 169 + x2 - 28x + 196 = x2 - 24x + 144
2x2 - 54x + 365 = x2 - 24x + 144
x2 - 30x + 221 = 0
x2 - 30x + 221 = 0
Solve by factoring.
x2 - 13x - 17x + 221 = 0
x(x - 13) - 17(x - 13) = 0
(x - 13)(x - 17) = 0
x - 13 = 0 or x - 17 = 0
x = 13 or x = 17
x = 13 can not be accepted.
Because, if x = 13, the side represented by (x - 14) is negative. So, x = 17.
Therefore, the length of each side of the equilateral triangle is 17 units.
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
10 Hard SAT Math Questions (Part - 40)
Dec 25, 25 08:30 AM
10 Hard SAT Math Questions (Part - 40) -
10 Hard SAT Math Questions (Part - 41)
Dec 24, 25 07:58 PM
10 Hard SAT Math Questions (Part - 41) -
ASTC Formula in Trigonometry
Dec 23, 25 11:34 PM
ASTC Formula in Trigonometry - Concepts - Examples and Solved Problems


