PYTHAGOREAN TRIPLE GENERATOR

Let us consider the right triangle shown below. 

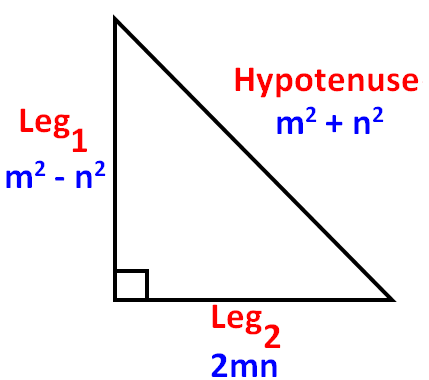
We can use the following formulas to generate a Pythagorean triple.  

Hypotenuse  =  m² + n²

Leg₁  =  m² - n²

Leg₂  =  2mn 

In the above formulas, always m has to be greater than n. 

That is, 

m > n

In the above formulas, we can take any positive values for m and n to get the three sides of a right triangle such that m > n. 

For example, let m  =  3 and  n  =  2. 

Then, we have

Hypotenuse   =   m² + n²  =  3² + 2²  =  9 + 4  =  13

Leg₁   =   m² - n²  =  3² - 2²  =  9 - 4  =  5

Leg₂   =   2mn  =  2(3)(2)  =  12

Now, we can check whether 13, 5, 12 be the three sides of the right angle triangle using Pythagorean theorem.

That is,

(Hypotenuse)²   =   (Leg₁)² + (leg₂)²

13²   =   5² + 12²

169  =  25 + 144

169  =  169

The three values 13, 5 and 12 satisfy the Pythagorean Theorem. 

Therefore, the values 13, 5 and 12 form a Pythagorean triple. 

How to Get the Sides of a Right Triangle

Example 1 : 

Using 5 and 6, create the lengths of three sides of a right triangle. 

Solution :

Since m > n, we can take m  =  6 and n  =  5. 

Then, we have

Hypotenuse   =   m² + n²  =  6² + 5²  =  36 + 25  =  61

Leg₁   =   m² - n²  =  6² - 5²  =  36 - 25  =  11

Leg₂   =   2mn  =  2(6)(5)  =  60

So, the lengths of three sides of the right triangle are

61,  11  and  60

Example 2 : 

Using 4 and 3, create the lengths of three sides of a right triangle. 

Solution :

Since m > n, we can take m  =  4 and n  =  3. 

Then, we have

Hypotenuse   =   m² + n²  =  4² + 3²  =  16 + 9  =  25

Leg₁   =   m² - n²  =  4² - 3²  =  16 - 9  =  7

Leg₂   =   2mn  =  2(4)(3)  =  24

So, the lengths of three sides of the right triangle are

25,  7  and  24

Example 3 : 

Using 1 and 2, create the lengths of three sides of a right triangle. 

Solution :

Since m > n, we can take m  =  2 and n  =  1. 

Then, we have

Hypotenuse   =   m² + n²  =  2² + 1²  =  4 + 1  =  5

Leg₁   =   m² - n²  =  2² - 1²  =  4 - 1  =  3

Leg₂   =   2mn  =  2(2)(1)  =  4

So, the lengths of three sides of the right triangle are

5,  3  and  4

Example 4 : 

Using 6 and 7, create the lengths of three sides of a right triangle. 

Solution :

Since m > n, we can take m  =  7 and n  =  6. 

Then, we have

Hypotenuse   =   m² + n²  =  7² + 6²  =  49 + 36  =  85

Leg₁   =   m² - n²  =  7² - 6²  =  49 - 36  =  13

Leg₂   =   2mn  =  2(7)(6)  =  84

So, the lengths of three sides of the right triangle are

85,  13  and  84

Example 5 : 

Using 11 and 6, create the lengths of three sides of a right triangle. 

Solution :

Since m > n, we can take m  =  11 and n  =  6. 

Then, we have

Hypotenuse   =   m² + n²  =  11² + 6²  =  121 + 36  =  157

Leg₁   =   m² - n²  =  11² - 6²  =  121 - 36  =  85

Leg₂   =   2mn  =  2(11)(6)  =  132  

So, the lengths of three sides of the right triangle are

157,  85  and  132

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.