PYTHAGOREAN THEOREM
In this section, we are going to study one of the most famous theorems in mathematics — the Pythagorean Theorem. The relationship it describes has been known for thousands of years.
Theorem :
In a right triangle, the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the other two legs.
It has been illustrated in the diagram shown below.
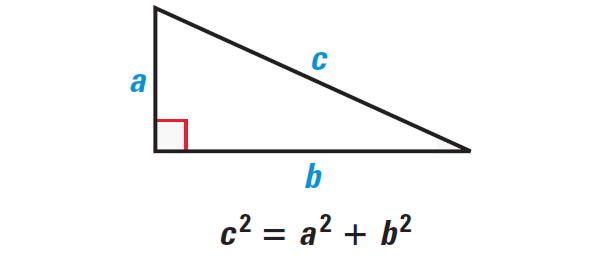
Proving the Pythagorean Theorem
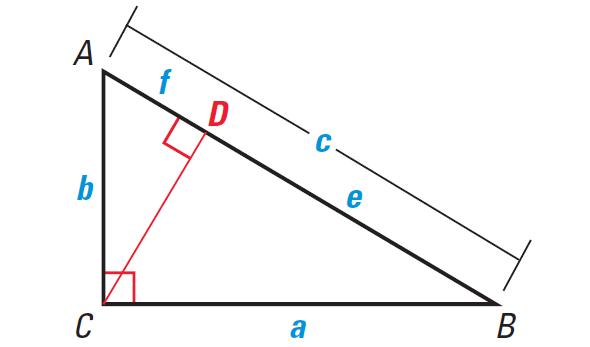
There are many different proofs of the Pythagorean Theorem. One is shown below.
Given : In ΔABC, ∠BCA is a right angle.
Prove : a2 + b2 = c2
Plan for Proof :
Draw altitude CD to the hypotenuse. Then apply Geometric Mean Theorem, which states that when the altitude is drawn to the hypotenuse of a right triangle, each leg of the right triangle is the geometric mean of the hypotenuse and the segment of the hypotenuse that is adjacent to that leg.
Using Pythagorean Theorem
A Pythagorean triple is a set of three positive integers a, b, and c that satisfy the equation
c2 = a2 + b2
For example, the integers 3, 4 and 5 form a Pythagorean triple.
Because,
52 = 32 + 42
Finding the Length of a Hypotenuse
Example :
Find the length of the hypotenuse of the right triangle shown below. Tell whether the side lengths form a Pythagorean triple.
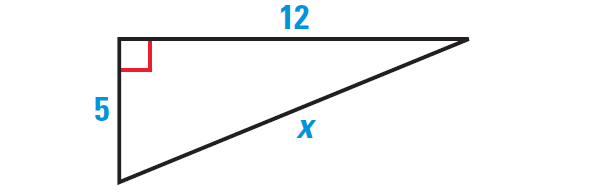
Solution :
By Pythagorean Theorem, we have
(Hypotenuse)2 = (leg)2 + (leg)2
Substitute.
x2 = 52 + 122
Simplify.
x2 = 25 + 144
x2 = 169
Take square root on each side.
√x2 = √169
x = 13
So, the length of the hypotenuse is 13 units.
Because 132 = 122 + 52, they form a Pythagorean triple.
Finding the Length of a Leg
Example :
Find the length of the leg of the right triangle shown below.
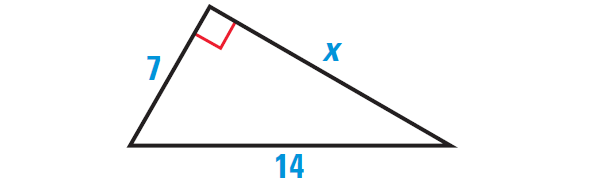
Solution :
By Pythagorean Theorem, we have
(Hypotenuse)2 = (leg)2 + (leg)2
Substitute.
142 = 72 + x2
Simplify.
196 = 49 + x2
Subtract 49 from each side.
147 = x2
Take square root on each side.
√147 = √x2
√147 = x
Use product property.
√49 ⋅ √3 = x
Simplify the radical.
7√3 = x
Hence, the required side length is 7√3 units.
Finding the Area of a Triangle
Example :
Find the area of the triangle to the nearest tenth of a meter.
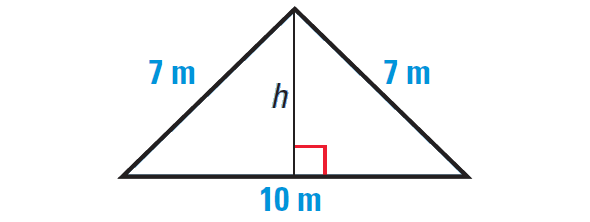
Solution :
We are given that the base of the triangle is 10 meters, but we do not know the height h.
Because the triangle is isosceles, it can be divided into two congruent right triangles with the given dimensions. Use the Pythagorean Theorem to find the value of h.
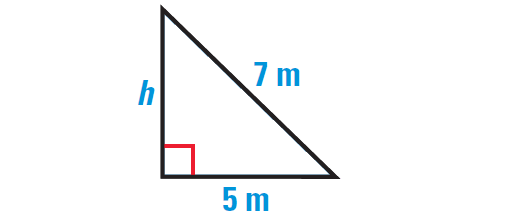
By Pythagorean Theorem, we have
72 = 52 + h2
Simplify.
49 = 25 + h2
Subtract 25 from each side.
24 = h2
Take square root on each side.
√24 = √h2
√24 = h
Now find the area of the original triangle.
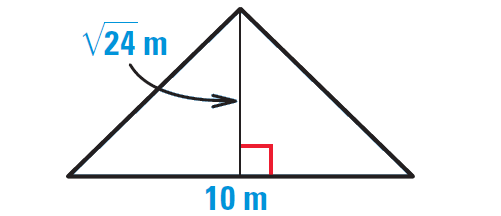
Area = 1/2 ⋅ b ⋅ h
Substitute.
Area = 1/2 ⋅ 10 ⋅ √24
Use calculator to approximate.
Area = 1/2 ⋅ 10 ⋅ √24
Area ≈ 24.5 m2
Hence, the area of the triangle is about 24.5 m2.
Apart from the stuff given above, if you need any other stuff in math, please use our google custom search here.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
WORD PROBLEMS
Word problems on simple equations
Word problems on linear equations
Word problems on quadratic equations
Area and perimeter word problems
Word problems on direct variation and inverse variation
Word problems on comparing rates
Converting customary units word problems
Converting metric units word problems
Word problems on simple interest
Word problems on compound interest
Word problems on types of angles
Complementary and supplementary angles word problems
Markup and markdown word problems
Word problems on mixed fractions
One step equation word problems
Linear inequalities word problems
Ratio and proportion word problems
Word problems on sets and Venn diagrams
Pythagorean theorem word problems
Percent of a number word problems
Word problems on constant speed
Word problems on average speed
Word problems on sum of the angles of a triangle is 180 degree
OTHER TOPICS
Time, speed and distance shortcuts
Ratio and proportion shortcuts
Domain and range of rational functions
Domain and range of rational functions with holes
Graphing rational functions with holes
Converting repeating decimals in to fractions
Decimal representation of rational numbers
Finding square root using long division
L.C.M method to solve time and work problems
Translating the word problems in to algebraic expressions
Remainder when 2 power 256 is divided by 17
Remainder when 17 power 23 is divided by 16
Sum of all three digit numbers divisible by 6
Sum of all three digit numbers divisible by 7
Sum of all three digit numbers divisible by 8
Sum of all three digit numbers formed using 1, 3, 4
Sum of all three four digit numbers formed with non zero digits
Sum of all three four digit numbers formed using 0, 1, 2, 3
Sum of all three four digit numbers formed using 1, 2, 5, 6
©All rights reserved. onlinemath4all.com
Recent Articles
-
Linear Growth and Decay
May 22, 22 03:05 AM
Linear Growth and Decay
-
Worksheet on Probability
May 22, 22 01:15 AM
Worksheet on Probability
-
Probability Worksheet
May 22, 22 01:12 AM
Probability Worksheet