PYTHAGOREAN THEOREM WORD PROBLEMS

Problem 1 :

One of the diagonals of a rectangle is 20 cm long. If the difference between its length and width is 4 cm, then find the area of the rectangle. 

Solution :

Let x be the length of the rectangle. 

Because the difference between its length and width is 4 cm, its width must be either (x + 4) cm or (x - 4) cm. 

Let's take the width as (x + 4) cm. 

Draw a sketch. 

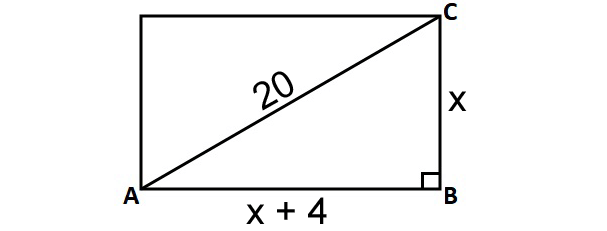
In the right triangle, according to Pythagorean theorem, we have 

(x + 4)²  + x²  =  20²

Simplify.

x² + 2(x)(4) + 4² + x²  =  400

x² + 8x + 16 + x²  =  400

2x² + 8x + 16  =  400

Subtract 400 from each side. 

2x² + 8x - 384  =  0

Divide each side by 2. 

x² + 4x - 192  =  0

(x + 16)(x - 12)  =  0

x + 16  =  0     or     x - 12  =  0

x  =  -16     or     x  =  12

Because the length of a rectangle can never be a negative value, we can ignore x  =  -16. 

So, the value of x is 12.

Then, 

x + 4  =  12 + 4

x + 4  =  16

Therefore,

length  =  12 cm 

width  =  16 cm

Area of the triangle :

=  l ⋅ w

=  12 ⋅ 16

=  192 cm²

So, the area of the rectangle is 192 square cm. 

If the height of a triangle is 17 inches less than the length of its base and the length of the hypotenuse is 25 inches, find the base and the height.

Problem 2 :

If the height of a triangle is 17 inches less than the length of its base and the length of the hypotenuse is 25 inches, find the base and the height.

Solution :

Draw a sketch.

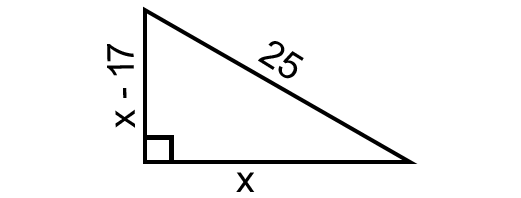
In the right triangle above, according to Pythagorean theorem, we have 

(x - 17)²  + x²  =  25²

Simplify.

x² - 2(x)(17) + 17² + x²  =  625

x² - 34x + 289 + x²  =  625

2x² - 34x + 289  =  625

Subtract 625 from each side. 

2x² - 34x - 336  =  0

Divide each side by 2. 

x² - 17x - 168  =  0

(x + 7)(x - 24)  =  0

x + 7  =  0     or     x - 24  =  0

x  =  -7     or     x  =  24

Because the base of a triangle can never be a negative value, we can ignore x  =  -7. 

So, the value x is 24.

Then, 

x - 17  =  24 - 17

x - 17  =  7

So, the base and height of the right triangle are 24 inches and 7 inches respectively. 

Problem 3 :

The sides of an equilateral triangle are shortened by 12 units, 13 units, 14 units respectively and a right angle triangle is formed. Find the length of side of the equilateral triangle. 

Solution :

Let x be the length of side of the equilateral side. 

Given : The sides of an equilateral triangle are shortened by 12 units, 13 units, 14 units and a right angle triangle is formed.  

Then, new lengths of the triangle  are

(x - 12), (x - 13) and (x - 14)

These are the sides of a right angle triangle and (x - 12) is the longest side. 

Draw a sketch. 

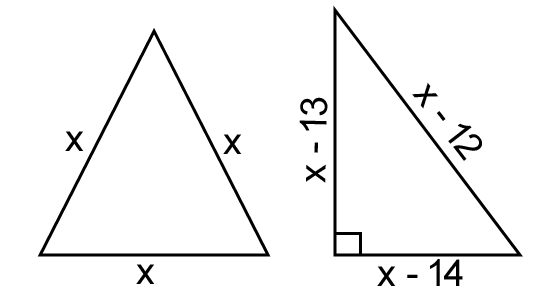
Because the longest side of the right triangle is hypotenuse, (x - 12) can be considered to be the length of the hypotenuse. 

According to Pythagorean theorem, the square of the hypotenuse is equal to sum of the squares of other two sides.

Then, we have ,  

(x - 13)² + (x - 14)²  =  (x - 12)²

x² - 2(x)(13) + 13² + x² - 2(x)(14) + 14²  =  x² - 2(x)(12) + 144

x² - 26x + 169 + x² - 28x + 196  =  x² - 24x + 144

2x² - 54x + 365  =  x² - 24x + 144

 x² - 30x + 221  =  0

(x - 13)(x - 17)  =  0

x  =  13  or  x  =  17

If we take x  =  13, the sides of the right triangle are

x - 12  =  1,   x - 13  =  0,  x - 14  =  -1

When x  =  13, we get one of the sides is zero and the sign of the another side is negative.  

Then, x  = 13 can not be accepted.

If we take x  =  17, the sides of the right triangle are

x - 12  =  5,   x - 13  =  4,  x - 14  =  3

All of the three sides of the right angle are positive when x  =  17.

Moreover, the lengths 5, 4 and 3 satisfy the Pythagorean theorem.  

That is,

5²  =  4² + 3²

25  =  16 + 9

25  =  25

Therefore, x  =  17 can be accepted. 

So, the length of side of equilateral triangle is 17 units. 

Problem 4 :

The base of a right triangle is 32 cm greater than its height and the hypotenuse is 7 cm greater than its base. Find the lengths of the three sides of the right triangle.  

Solution :

Let x be the height of the right triangle. 

Then, we have 

Base  =  x + 32

Hypotenuse  =  (x + 32) + 8  =  x + 40

Draw a sketch. 

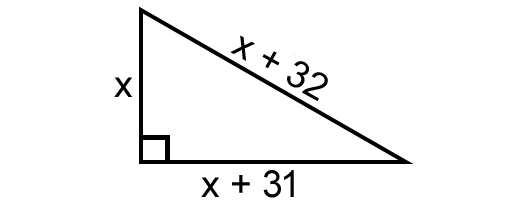
In the right triangle above, according to Pythagorean theorem, we have 

x² + (x + 31)²  =  (x + 32)²

Simplify.

x² + x² + 2(x)(31) + 31²  =  x² + 2(x)(32) + 32²

2x² + 62x + 961  =  x² + 64x + 1024

x² - 2x - 63  =  0

Factor. 

(x + 7)(x - 9)  =  0

x + 7  =  0     or     x - 9  =  0

x  =  -7     or     x  =  9

Because the height of a triangle can never be a negative value, we can ignore x  =  -7. 

So, the value x is 9.

Then, 

x + 31  =  9 + 31  =  40

x + 32  =  9 + 32  =  41

So, the lengths of the three sides of the right triangle are 9cm, 40 cm and 41 cm. 

Problem 5 :

From a train station, one train heads north, and another heads east. Some time later, the northbound train has traveled 12 miles, and the eastbound train has traveled 16 miles. How far apart are the two trains, measured in a straight line ?

Solution :

Let the two trains be x miles apart.

Draw a sketch.

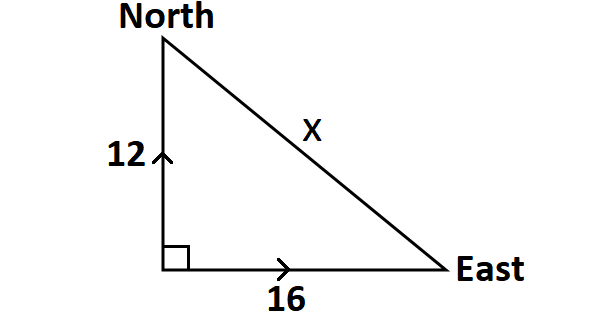
In the right triangle above, according to Pythagorean theorem, we have 

x²  =  12² + 16²

Simplify and solve for x. 

x²  =  144 + 256

x²  =  400

x²  =  20²

x  =  20

So, the two trains are 20 miles apart. 

Problem 6 : 

The three sides of a right triangle are in the ratio 3 : 4 : 5 and the area of the triangle is 24 square cm. Find the sides of the triangle. 

Solution : 

From the given ratio 3 : 4 : 5, the sides of the triangle can be assumed as 

3x, 4x, 5x

Always the longest side of the right triangle is hypotenuse. 

Then, the length of the hypotenuse is 5x. 

Draw a sketch. 

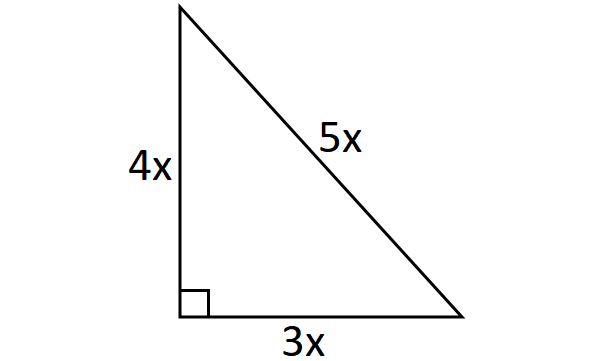
In the right triangle above, the base is 3x and the height is 4x. 

Given : Area of the triangle is 24 square cm. 

Area  =  24 cm²

Write the formula for area of triangle. 

1/2 ⋅ base ⋅ height  =  24

Substitute 3x for base and 4x for height. 

1/2 ⋅ 3x ⋅ 4x  =  24

6x²  =  24

Divide each side by 6. 

x²  =  4

x²  =  2²

x  =  2

Then, we have 

3x  =  3(2)  =  6

4x  =  4(2)  =  8

5x  =  5(2)  =  10

So, the three sides of the triangle are 6 cm, 8 cm and 10 cm. 

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.