PYTHAGOREAN THEOREM WORD PROBLEMS WORKSHEET
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Problem 1 :
The bottom of a ladder must be placed 3 feet from a wall. The ladder is 12 feet long. How far above the ground does
the ladder touch the wall? Round your answer to the nearest tenth.
Problem 2 :
What is the length of the diagonal of a 10 cm by 15 cm rectangle? Round your answer to the nearest integer.
Problem 3 :
A soccer field is a rectangle 90 meters wide and 120 meters long. The coach asks players to run from one corner to the corner diagonally across the field. How far do the players run?
Problem 4 :
How far from the base of the house do you need to place a 15' ladder so that it exactly reaches the top of a 12' wall?
Problem 5 :
The diagonal of a rectangle is 25 in. The width is 15 in. What is the area of the rectangle?
Problem 6 :
An isosceles triangle has congruent sides of 20 cm. The base is 10 cm. What is the area of the triangle? Round your answer to the nearest tenth.
Problem 7 :
A baseball diamond is a square that is 90’ on each side. If a player throws the ball from 2nd base to home, how far will the ball travel? Round your answer to the nearest tenth.
Problem 8 :
Jill’s front door is 42” wide and 84” tall. She purchased a circular table that is 96 inches in diameter. Will the table
fit through the front door?

Answers
1. Answer :
Let the ladder touch the wall x ft. above the ground.
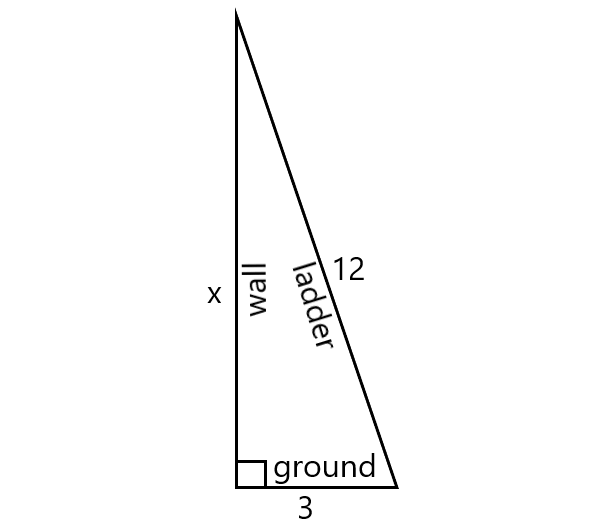
Using Pythagorean Theorem,
x2 + 32 = 122
x2 + 9 = 144
Subtract 9 from both sides.
x2 = 135
Take square root on both sides.
x = √135
x ≈ 11.6
Therefore, the ladder touches the wall 11.6 ft. above the ground.
2. Answer :
Let x be the length of the diagonal of the rectangle.
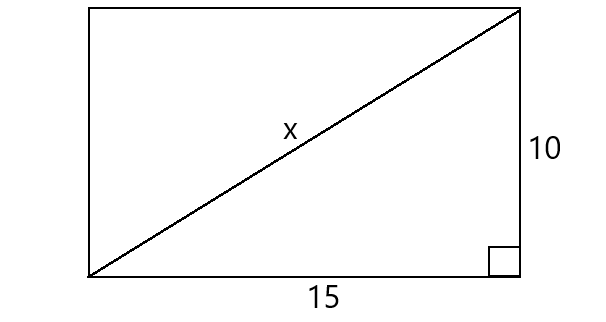
Using Pythagorean Theorem,
x2 = 152 + 102
x2 = 225 + 100
x2 = 325
Take square root on both sides.
x ≈ 18
Therefore, the length of the diagonal is 18 cm.
3. Answer :
Let x represent the distance from one corner to the corner diagonally across the field.
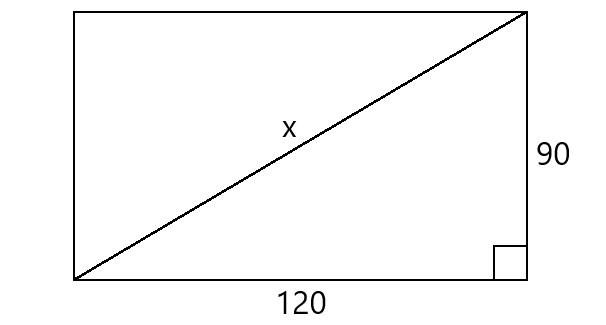
Using Pythagorean Theorem,
x2 = 902 + 1202
x2 = 8100 + 14400
x2 = 22500
Take square root on both sides.
x = 150
Therefore, the players run 150 m.
4. Answer :
Let the ladder be placed x ft. from the base of the house.
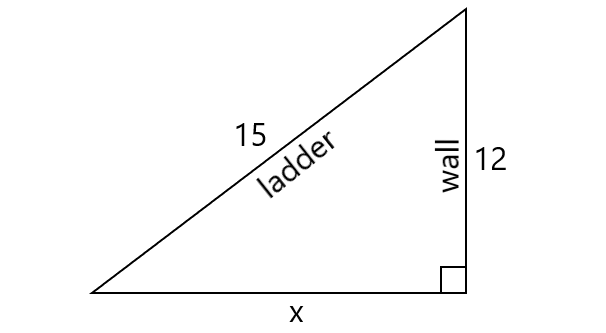
Using Pythagorean Theorem,
x2 + 122 = 152
x2 + 144 = 225
Subtract 144 from both sides.
x2 = 81
Take square root on both sides.
x = 9
Therefore, the ladder has to be placed 9 ft. from the base of the house.
5. Answer :
Given :
Diagonal = 25 in.
Width = 15 in.
To find the area of the rectangle, we need the length.
Let x represent the length of the rectangle.
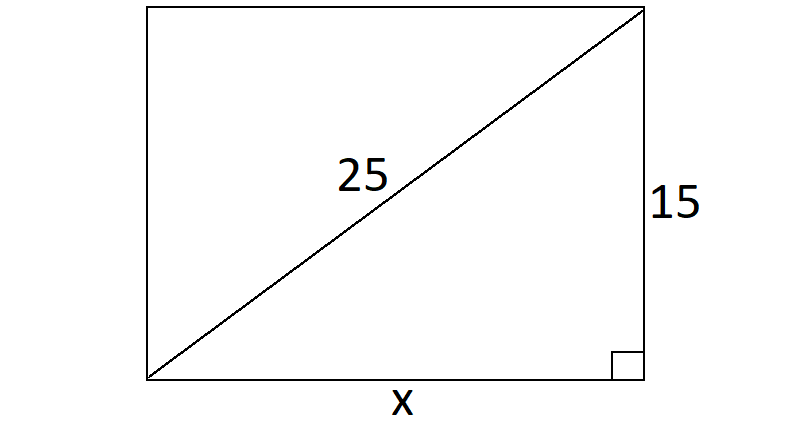
Using Pythagorean Theorem,
x2 + 152 = 252
x2 + 225 = 625
Subtract 225 from both sides.
x2 = 400
Take square root on both sides.
x = 20
The length of the rectangle is 20 in.
Area of the rectangle :
= length x width
= 15 x 25
= 375 in.2
6. Answer :
In an isosceles triangle, an altitude drawn between the two congruent sides will bisect the third side.
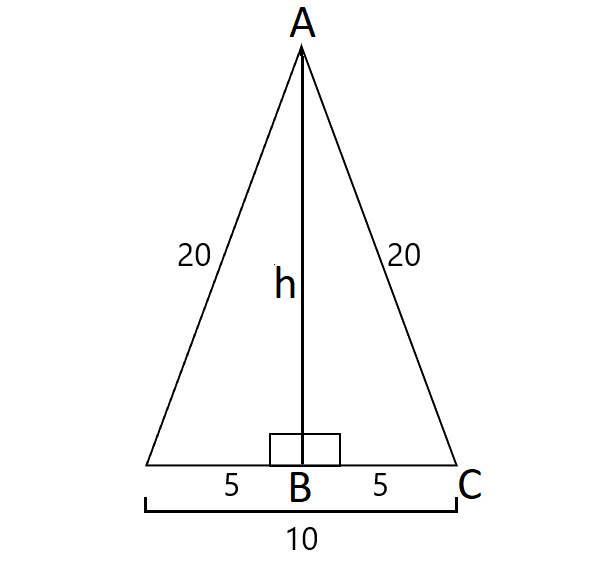
In the right triangle ABC, using Pythagorean Theorem,
h2 + 52 = 202
h2 + 25 = 400
Subtract 25 from both sides.
h2 = 375
Take square root on both sides.
h = √375
Area of the triangle :
= ½ x base x height
= ½ x 10 x √375
≈ 96.8 cm2
7. Answer :
Let x represent the distance traveled by the baseball from the 2nd base to home.
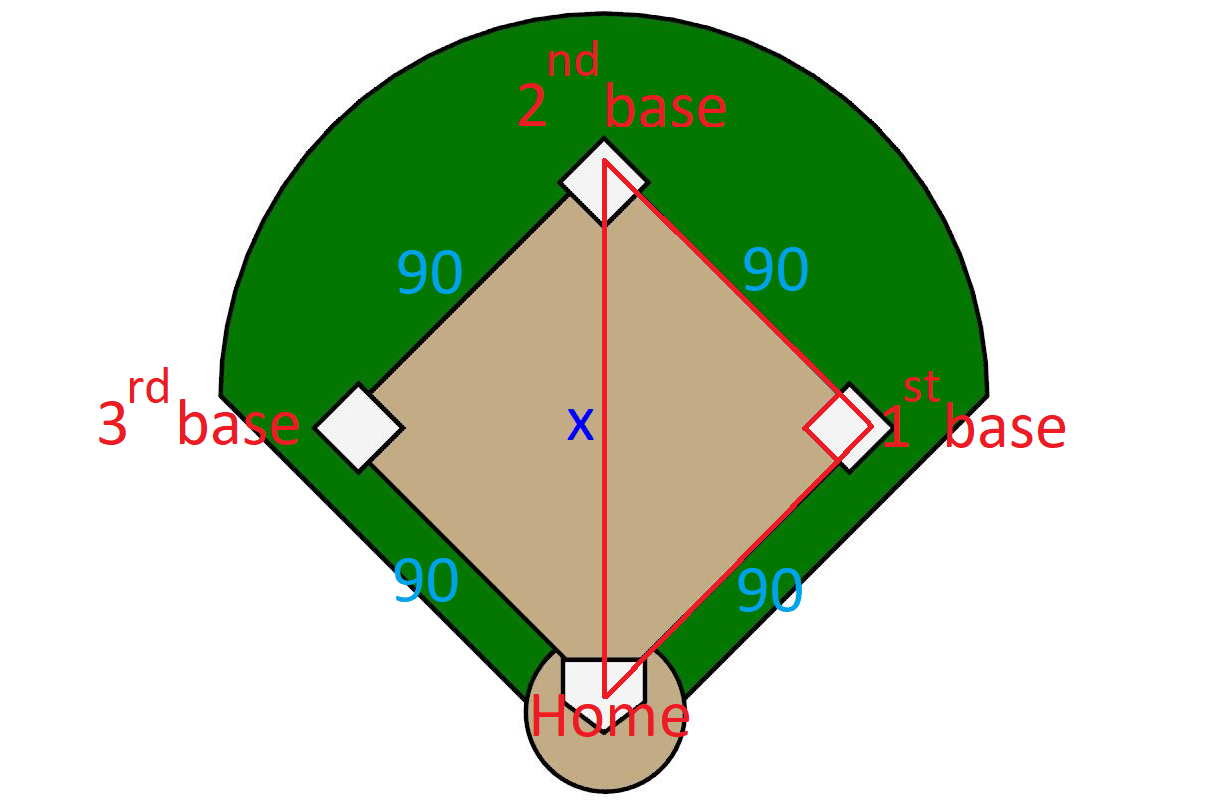
Using Pythagorean Theorem,
x2 = 902 + 902
x2 = 8100 + 8100
x2 = 16200
Take square root on both sides.
x ≈ 127.3 ft.
8. Answer :
The width of the door is 42” and the length is 84”. A circular table that is 96" in diameter can fit through width or length. Because both width and length are less than 96". If the diagonal of the door is greater than 96", the circular table can fit through the diagonal.
Let x represent the diagonal.
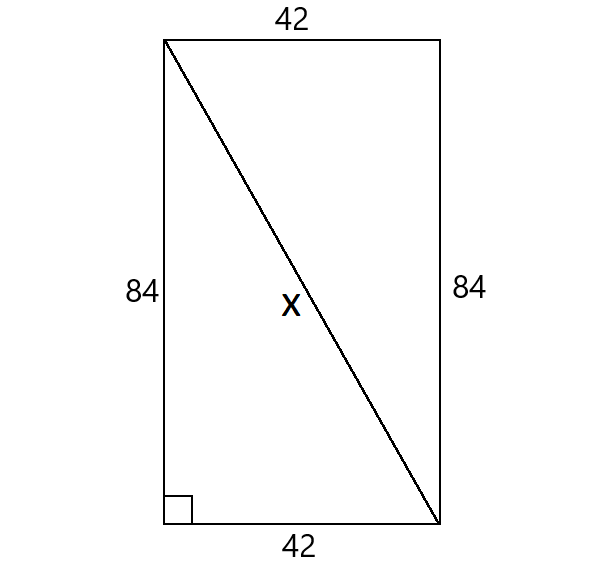
Using Pythagorean Theorem,
x2 = 842 + 422
x2 = 7056 + 1764
x2 = 8820
Take square root on both sides.
x ≈ 94"
The diagonal of the door is 94", which is less than the diameter of the circular table 96"
Therefore, the table will not fit through the front door.
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
10 Hard SAT Math Questions (Part - 45)
Jan 19, 26 06:14 AM
10 Hard SAT Math Questions (Part - 45) -
10 Hard SAT Math Questions (Part - 44)
Jan 12, 26 06:35 AM
10 Hard SAT Math Questions (Part - 44) -
US Common Core K-12 Curricum Algebra Solving Simple Equations
Jan 07, 26 01:53 PM
US Common Core K-12 Curricum Algebra Solving Simple Equations