PSAT SAMPLE QUESTIONS WITH ANSWERS

Question 1 :

If Anthony and Bridget take turns watching T.V every 4 hours and Anthony's third watch was at 10 : 00 P.M and Bridget was the first to watch T.V, then when did Bridget begin her second watch ?

(A)  6:00 P.M  (B)  2:00 P.M  (C)  10:00 A.M

(D)  10:00 P.M  (E)  6:00 A.M

Solution :

For every 4 hours the turn is going to be changed between Anthony and Bridget.

By calculating this, we get the following schedule 

(Third Watch)

From 2 : 00 P.M to 10 : 00 P.M  --> Anthony 

(Second Watch)

From 10 : 00 A.M to 2 : 00 P.M  --> Bridget

So, Bridget will get second chance to watch T.V at 10 : 00 A.M.

Question 2 :

There is a total of 9 bicycles and unicycles in a path. There are 13 wheels in total. If x is the number of bicycles, what is x² ?

(A)  16  (B)  12  (C)  23  (D)  13  (E)  9

Solution :

Let x and y be the number of bicycles and unicycles.

Each bicycle will have "2 wheels"

Each unicycles will have "1 wheel"

Total number of cycles  =  9 ==>  x + y  =  9 -------(1)

Number of wheels in cycles  =  13

2x + 1y  =  13 -------(2)

(1)  - (2)

x + y - (2x + y)  =  9 - 13

-x  =  -4

x  =  4

x²  =  4²  ==>  16

Question 3 :

A boy moves 4 miles south, Then he turns 90 degree to the left. He moves forward 6 miles. He turns 90 degree to the left. He moves forward 4 miles. How far is he now than from his starting point ?

(A)  4 miles   (B)  3 miles  (C)  6 miles

(D)  5 miles (E)  8 miles

Solution :

By drawing a picture from the given details, we get

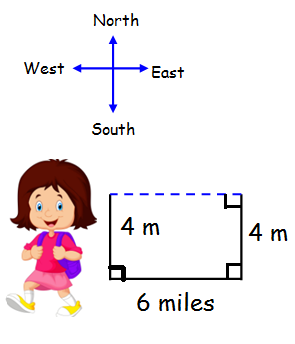
Hence he is 6 miles away from the starting point.

Question 4 :

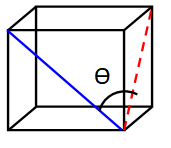
The angle is between two diagonal lines of the cube.

In the figure, what is θ

(A)  45  (B)  56  (C)  60  (D)  90  (E)  30

Solution :

In a cube, length of diagonals will be equal.

The diagonal at the front face, diagonal at the side face and the diagonal at the top will be equal.

Th triangle formed by these diagonals will be equilateral triangle. So, the angle between two diagonals is 60 degree.

Question 5 :

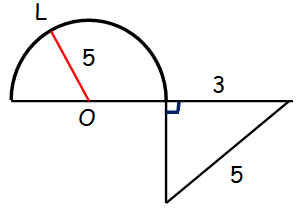
OL is the radius. What is the perimeter of the figure above ?

(A)  12 + 5π     (B)  12 + 25π     (C)  6 + 25π 

(D)  22 + 5π    (E)  22 + 25π

Solution :

The picture given above consists of two shapes, a semi circle and a triangle.

Perimeter of semicircle  =  (π + 2)r

Perimeter of triangle  =  sum of length of all sides

Perimeter of semicircle  =  (π + 2)(5)

  =  5π + 10  ---(1)

Let "x" be the unknown side of the triangle.

5²  =  x² + 3²

x²  =  25 - 9  =  16  ==> 4

Perimeter of triangle  =  4 + 5 + 3  =  12  -----(2)

Perimeter of the given shape  =  5π + 10 + 12 

  =  5π + 22

Question 6 :

What is 0.53 bar - 0.36 bar?

(A)  7/50  (B)  17/100  (C)  7/99  (D)  17/99  (E)  7/9

Solution :

x = 0.5353..............  -----(1)

Multiply by 100 on both sides

100 x = 53.53.............. -----(2)

(2) - (1)

99 x  =   53

x  =  53/99

y  =  0.3636..............  -----(1)

Multiply by 100 on both sides

100 y  =  36.36.............. -----(2)

(2) - (1)

99 y  =   36

y  =  36/99

x - y  ==>  (53/99) - (36/99)

  =  17/99

Hence the answer is 17/99.

Question 7 :

The sum of two positive numbers is 6 times their difference. What is the ratio of the reciprocal of larger number to the reciprocal of smaller number ?

(A)  5/7  (B)  7/5  (C)  5/2  (D)  2/5  (E)  9/5

Solution :

Let x be larger number and y be the smaller number.

x + y  =  6 (x - y) ---(1)

Ratio of the reciprocal of larger to the smaller.

(1/x) : (1/y)  ==>  y/x

From (1) 

x + y  =  6x - 6y

-5x  =  -7y

x/y  =  7/5

y/x  =  5/7

Hence the ratio of the reciprocal of larger number to the reciprocal of smaller number is 5/7.

Question 8 :

The mean weekly salary of 9 teachers in a school is $1,000. If there are 9 teachers and 11 assistant principals and the mean weekly salary for assistant principals and teachers is $1,275, what is the mean salary of the assistant principals ?

(A)  $1,100  (B) $1,500  (C) $1,137.50 

(D) $1,300  (E) $1,000

Solution :

Mean weekly salary of 9 teachers  =   $1,000

Sum of salary of 9 teachers / 9  =  1000

Sum of salary of 9 teachers  =  9000

Let y be the sum of salary of 11 assistant principals.

(9000 + y)/(9 + 11)  =  1275

(9000 + y)/20  =  1275

9000 + y  =  1275(20)

9000 + y  =  25500

y  =  25500 - 9000

  y  =  16500

Mean salary  =  16500/11

=  $1500

Question 9 :

Given  x_n  =  x_{n - 1} + x_n-2, what is x₆/x₅, knowing that x₄  =  3 and x₃  =  2?

(A)  3/2  (B)  5/8  (C)  8/5  (D)  2/3  (E)  13/5

Solution :

 x₆/x₅  =  8/5

Question 10 :

f(x)  =  (1 - x)/(x - 1), which of the following set is not a possible domain for the given function ?

(A)  {2, 3, 5}  (B)  {1, 0 , 6}  (C)  {π, 2.17, 10}

(D)  {2π, π², 0.65}  (E)  {4, 6, 10}

Solution :

The set which contains the number 1 is not a possible domain.

f(1)  =  (1 - 1)/(1 - 1) is not possible.

Hence the answer is {1, 0, 6}.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.