PSAT SAMPLE QUESTIONS ONLINE

Question 1 :

 √100 √64  =  

(A)  8  (B)  10  (C)  18  (D)  80  (E)  164

Solution :

 √100 √64  =   √(10 ⋅ 10) √(8 ⋅ 8)

  =  10 (8)

  =  80

Hence the answer is 80.

Question 2 :

7.2 aliens  =  1 monster

1 monster  =  15.5 oranges

Using the conversion above, how many oranges are equal to 1 alien ?

(A)  0.46  (B)  1.95  (C)  2.15  (D)  22.7  (E)  111.6

Solution :

1 monster  =  7.2 aliens   ----(1)

1 monster  =  15.5 oranges  ----(2)

(1)  =  (2)

7.2 aliens  =  15.5 oranges

1 alien  =  15.5/7.2

=  2.15

Hence the answer is 2.15

Question 3 :

What is the greatest common factor of 147 and 198 ?

(A)  2  (B)  3  (C)  7  (D)  14  (E)  49

Solution :

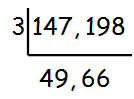
There is no common divisor for 49 and 66. Hence the greatest common factor is 3.

Question 4 :

If x  =  7 and y  =  0, what is the value of 11x / (x - y) ?

(A)  0  (B)  7  (C)  10  (D)  11  (E)  77

Solution :

11x / (x - y)  =  11(7) / (7 - 0)  ==>  77/7  ==>  11

Hence the answer is 11.

Question 5 :

Heiga has 4 dogs, 3 cats and 2 birds. If she closes her eyes and picks one animal. What is the probability that it does not have 4 legs ?

(A)  3u/7  (B)  2/7  (C)  7/9  (D)  2/9  (E)  4/7

Solution :

Sample space  =  Total number of animals 

  =  3 + 4 + 2

n(S)  =  9

Dogs and cats have 4 legs, and birds has 2 legs.

Number of animals do not have 4 legs  =  2 

n(A)  =  2

P(A)  =  n(A) / n(S)

P(A)  =  2/9

Hence the required probability is 2/9.

Question 6 :

If y = x²⋅x^x, what is y when x = 2 ?

(A)  16  (B)  8  (C)  4  (D)  32  (E)  0

Solution :

y  =  x²⋅x^x

y  =  x^{(2 + x)}

y  =  2^{(2 + 2)}

y  =  2⁴

y  =  16

Hence the answer is 16.

Question 7 :

Train A, travelling at 200 mph, leaves station A at 1 P.M train B travelling at 300 mph, leaves station B at 3 P.M. Both stations are directly across each other and X miles away. If the trains meet at 4 P.M, What is X ?

(A)  500 ml  (B)  900 ml  (C)  700 ml 

(D)  600 ml  (E)  400 ml

Solution :

From the given information, we know that both trains meet at 4 P.M.

Train A has traveled for 3 hours at the speed of 200 mph

Train B has traveled for 1 hour at the speed of 300 mph

Distance covered by both trains together 

=  600 miles + 300 miles

  =  900 miles

Hence both trains will meet each other apart 900 miles.

Question 8 :

Bernard is now y years old. Luis is 8 years older than Bernard. In terms of y, how old was Luis 5 years ago?

(A)  8y  (B)  8y - 5  (C)  y + 3  (D)  y + 13  (E)  y - 5

Solution :

Age of Bernard  =  y

Age of Luis  =  y + 8

5 years ago Luis age  =  y + 8 - 5

  =  y + 3

Question 9 :

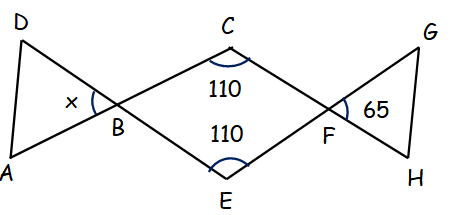
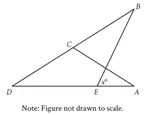
In a figure above, ABC, DBE, EFG and CFH are straight line segments. What is the value of x ?

(A)  25  (B)  45  (C)  65  (D)  70  (E)  75

Solution : 

In a quadrilateral BEFC,

<GFH  =  <EFC  =  65 (Vertically opposite angles)

<CBE + <BEF + <EFC + <FCB  =  360

<CBE + 110 + <EFC + 110  =  360

<CBE + 220 + 65  =  360

<CBE  =  360 - 285

<CBE  =  75

x =  <CBE  =  75 (Vertically opposite angles)

Question 10 :

Which of the following shows the fraction 13/3, 37/8 and 19/4 in order from greatest to least ?

(A)  37/8, 19/4, 13/3

(B)  37/8, 13/3, 19/4

(C)  19/4, 13/3, 37/8

(D)  19/4, 37/8, 13/3

(E)  13/3, 19/4, 37/8

Solution :

In order to arrange the fractions from greatest to least, first let us change the denominator same. For that, we have to find L.C.M of 3, 8 and 4.

L.C.M  =  24

(13/3) ⋅ (8/8)  =  104/24   -----(1)

(37/8) ⋅ (3/3)  =  111/24   -----(2)

(19/4) ⋅ (6/6)  =  114/24   -----(3)

19/4 > 37/8 > 13/3

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.