PSAT PRACTICE QUESTIONS MATH

Question 1 :

(-39)²/13³

Solution :

  =  (-39)²/13³

Since we have even power, so the negative sign will become positive.

=  (39 ⋅ 39) / (13 ⋅ 13 ⋅ 13)

=  (3 ⋅ 3) / 13

=   9/13

Question 2 : 

In a scaled diagram, 1 inch represents 20 feet. How many square inches on the diagram represent 1 square foot ?

Solution :

1 inch  =  20 feet

1 feet  =  1/20 inch

1 square foot  =  (1/20)²

  =  1/400

  =  0.0025

Hence 0.0025 square inches represents 1 square foot.

Question 3 :

What is the greatest common factor of 2,240 and 3,360 ?

Solution :

To find the greatest common factor, we have to decompose the given numbers into the prime factors until we get prime numbers.

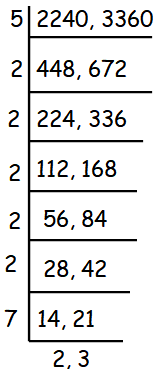
To find the greatest common divisor, take all the common divisors of 2240 and 3360 and multiply them.

Greatest common factor  =  5 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 7 

=  1120

Question 4 :

If 50% of 2y is 12, what is y² ?

Solution :

50% of 2y  =  12

(50/100) ⋅ (2y)  =  12

(1/2) ⋅ (2y)  =  12

y  =  12

y²  =  12²  ==>  144

Hence the value of y² is 144.

Question 5 :

(15)  In the figure given below ∢ PRL is 150 degree. What is (a² - b²)/(a - b) ?

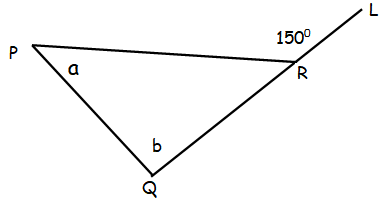
Solution :

To find the value of  (a² - b²)/(a - b), first let us simplify this using algebraic identities.

(a² - b²)/(a - b)  =  (a + b)(a - b)/(a - b)

(a² - b²)/(a - b)  =  a + b

From the given picture, we have 

<PRL  =  150

<PRL  =  <RPQ + <PQR

 150  =  a + b 

Hence the value of a + b is 150.

Question 6 :

If y = 3/4 and xy²  =  9/16, what is (x - 4)?

Solution :

Given that :

y = 3/4 and xy²  =  9/16

x(3/4)²  =  9/16

x(9/16)  =  9/16

x  =  1

then x - 4  =  1 - 4  =  -3

Hence the value of x - 4 is -3

Question 7 :

If P is an odd integer, which of the following must be an even number ?

Solution :

By observing the options, D is having an even number in the denominator. So we might have even number in the numerator.

Even number / even number  =  even number

Hence   (2p² - 2P³) / 2P is the even number.

Question 8 :

If the diameter of a circle is P, and P²/4  =  2, what is the area of the circle ?

Solution :

Diameter of the circle  =  P

Radius of the circle  =  P/2

Area of the circle  =  π r²

  =   π (P/2)²

  =   π (P²/4)

  =  2π

Hence the required area of the circle is 2π.

Question 9 :

If a regular polygon has (N - 10) sides, where, N = (40/10)², what is the measure of one of its angles?

Solution :

N = (40/10)²  ==>  4²  =  16

Number of sides in the given polygon 

N - 10  ==>  16 -  10  =  6

So, the given polygon has 6 sides, it is hexagon.

Sum of the angles of a polygon  =  (n - 2) 180

=  (6 - 2) 180

  =  4 (180)

=  720

Angle measure  =  720/6

 =  120 degree

Question 10 :

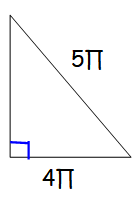
If the perimeter of the triangle shown above is the circumference of a circle, then what is the radius of the circle?

Solution :

Perimeter of triangle  =  Sum of lengths of all sides

Let "x" be the length of unknown side.

(5π)²  =  (4π)² + x²

25π² - 16π²  =  x²

x²  =  9π²

x  =  3π

Perimeter of triangle  =  3π + 5π + 4π

Circumference of circle  =  12 π

2π r  =  12π

r  =  6

Hence the radius of circle is 6

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.