PSAT MATH TEST

Question 1 :

If A  =  3r²h² and (rh) increases by 100%, then the new A is what times of the old A ?

Solution :

A  =  3r²h²

A  =  3(rh)²  ----(1)

rh increases by 100%  =  rh + 100% of rh

  =  rh + rh

  =  2rh

By applying the increase rate in (1)

A  =  3(2rh)²

A  =  3(4r²h²)

A  =  4(3r²h²)

Hence, the new A is 4 times of the old A.

Question 2 :

If x^a  =  ^q√x^p, what is p²/q² ?

Solution :

x^a  =  ^q√x^p

x^a  =  (x^p)^1/q

x^a  =  x^p/q

Since base are equal, powers are also equal

a  =  p/q

Taking squares on both sides, we get 

a²  =  (p/q)²

a²  =  p²/q²

Hence the value of p²/q² is a².

Question 3 :

Set A  =  {1, 2, 3, a} set B  =  {2, 4, 5, a², b}, what is AnB ?

Solution :

AnB is the set of common elements of both sets A and B.

AnB  =  { 2 }

Hence the answer is { 2 }.

Question 4 :

2√75 - (√25) (√3)

Solution :

2√75 - (√25) (√3)

  =  2√75 - √(25⋅3)

  =  2√75 - √75

  =  √75

  =  √(5⋅5⋅3)

  =  5 √3

Hence the answer is 5 √3

Question 5 :

Express 0.0345/10 in scientific notation.

Solution :

0.0345/10 

Since we have 10 in the denominator, we have to move the decimal point 1 digit to the left.

0.0345/10   =  0.00345

In order to represent in scientific notation, we have to move the decimal point three digits to the right side.

0.00345  =  3.45 x 10^-3 

Hence the answer is 3.45 x 10^-3.

Question 6 :

If q  =  x + y and x  =  y + z, what is z in terms of y and q ? 

Solution :

q  =  x + y -----(1)

x  =  y + z  ----(2)

From (2), 

z  =  x - y  ----(3)

From (1),

x  =  q - y

By applying the value of x in (3), we get

z  =  q - y - y

z  =  q - 2y

Question 7 :

y = x³

The only possible values of x are those in the set {-1/3, 1/2, 1/3} what is the maximum value of y ? 

Solution :

The largest element of the given set is 1/2. To get the maximum value of y, we have to apply 1/2 instead of x.

y = (1/2)³

y = 1/8

Hence the maximum value of y is 1/8.

Question 8 :

What is (x³y²z⁴) / (z³y³) equal to ?

Solution :

(x³y²z⁴) / (z³y³)  =  x³y^2-3 z^4-3

  =  x³y^-1 z¹

  =  x³z/y

Hence the answer is x³z/y.

Question 9 :

What is the length of RL ?

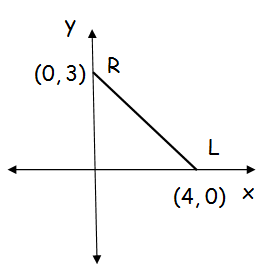
Solution :

To find the length of RL, we have to use the formula for distance between two points.

d  =  √(x₂ - x₁)² + (y₂ - y₁)²

 R(0, 3) L(4, 0)

d  =  √(4 - 0)² + (0 - 3)²

d  =  √4² + 3²

d  =  √(16 + 9)  =  √25

d = 5

Question 10 :

In a triangle, the first angle is two times the second angle and the second angle is three times the third angle. Find the measure of the third angle.  

Solution :

Let x be the measure of the third angle.

Then,

Measure of the second angle  =  3x

Measure of the second angle  =  2(3x)  =  6x

In a triangle, sum of the three angles is equal to 180°.

Then, 

6x + 3x + x  =  180°

10x  =  180°

Divide each side by 10.

x  =  18°

So, the measure of the third angle is 18°. 

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.