PSAT MATH QUESTIONS FOR PRACTICE

Question 1 :

[(2/3) + (1/4)]  ÷ 2  =

(A)  22/12  (B)  1/12  (C)  11/24  (D)  1/3  (E)  12

Solution :

  =  [(2/3) + (1/4)]  ÷ 2

  =  [(2/3) ⋅ (4/4) + (1/4) ⋅ (3/3)]  ÷ 2

  =  [(8/12) + (3/12)]  ÷ 2

  =  [(8 + 3)/12]  ÷ 2

  =  (11/12) ÷ (2/1)

  =  (11/12) ⋅ (1/2)

  =  11/24

Hence the answer is 11/24.

Question 2 :

Michelle bought a dress that costs $103.00, a pair of shoes that costs $73.00 and a bag that costs $111.00. There is a 7% sales tax on all items priced at $90.00 and higher. There is no sales tax on items under $90.00. How much did Michelle spend on the following items, including tax ?

(A)  $287.00  (B)  266.00  (C)  295.47 

(D)  300.60  (E)  $301.98

Solution :

Michelle bought three items.

A dress costs  =  $103.00

A pair of shoes costs  =  $73.00

A bag costs  =  $111.00

The cost of dress and bag are more than $90. So, we have to pay sales tax for those items.

Sales tax  =  7%

107% of cost of dress  =  1.07 (103.00)  =  110.21 

107% of cost of bag  =  1.07(111.00)  =  118.77

cost of shoes  =  73

Total cost  =  110.21 + 118.77 + 73

  =  301.98

Question 3 :

How many terms are in the sequence

0, 3, 6.............57, 60 ?

(A)  20  (B)  21  (C)  23  (D)  30  (E)  60

Solution :

a = 0, d = 3 - 0  ==>  3 and l  =  60

Total number of terms :

n = [(l - a)/d] + 1

n  =  [(60 - 0)/3] + 1

n  =  (60/3) + 1

n  =  20 + 1

n  =  21

Question 4 :

The larger of two consecutive even integers is two times the smaller. What is their sum ?

(A)  2  (B)  3  (C)  4  (D)  6  (E)  8

Solution :

Let "x" be a even number

Consecutive even number  =  x + 2

x + 2  =  2x

2x - x  =  2

x  =  2

So, the two even numbers are 2 and 4.

Their sum  =  2 + 4  =  6

Question 5 :

3^x  =  27 ^a+b and (a² - b²) /(a-b)  =  5, what is x ?

(A)  6  (B)  9  (C)  12  (D)  15  (E)  27

Solution :

First, let us simplify (a² - b²) / (a-b)

5  =  [(a + b) (a -b)] / (a - b)

  5  =  (a + b)

So, the value of a + b is 5.

3^x  =  27⁵ 

3^x  =  (3³)⁵ 

3^x  =  3¹⁵

Hence the value of x is 15.

Question 6 :

In Mr.Farmer's class there are 30 kids. If there are twice as many boys as there are girls in the English club, then what percentage of the English club are boys ?

(A)  2  (B)  3  (C)  4  (D)  6  (E)  8

Solution :

Let "x" be the number of girls in English club

"2x" be the number of boys

x + 2x  =  30

3x  =  30

x  =  10

2x  =  20 (number of boys)

Percentage of boys  =  (20/30) ⋅ 100

=  66.6%

Question 7 :

a⊗b  =  a³-3a²b + 3ab² - b³ and a ⊕b  =  (a-b)(a-b), what is (a⊗b) / (a⊕b)

(A)  a² + b²  (B)  a - b  (C) a² + 3b² + 3ab

(D)  a² - b²  (E)  b² + 3a

Solution :

a⊗b  =  a³-3a²b + 3ab² - b³   = (a - b)³

a ⊕ b  =  (a - b) (a - b)  =  (a-b)²

a⊗b/a⊕b  =  (a - b)³/ (a-b)² 

  =  (a - b)

Question 8 :

What is the prime factorization of 752 ?

(A) 2³ ⋅ 48  (B) 2³ ⋅ 49  (C) 3³ ⋅ 49 

 (D) 2⁴ ⋅ 47  (E) 3⁴ ⋅ 47

Solution :

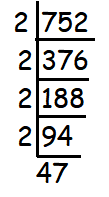
752  =  2⁴ ⋅ 47

Question 9 :

If x can be any integer, what is least possible value of the expression 4x² - 10 ?

(A)  -10  (B)  -4  (C)  4  (D)  10  (E)  ∞

Solution :

By applying any negative value for x, we get positive value for x²

The least value may appear, when x = 0

  =  4(0)² - 10

  =  -10

Hence the answer is -10.

Question 10 :

There is a total of 5 bicycles and tricycles in a park. There are 12 wheels. How many tricycles are there ?

(A)  2  (B)  3  (C)  6  (D)  7  (E)  8

Solution :

Let us use the concept system of equations to solve this problem.

Total number of vehicles  =  5

Let x be the number of bicycles

Let y be the number of tricycles.

Each bicycle will have 2 wheels and tricycle will have 3 wheels.

x + y  =  5   -----(1)

2x + 3y  =  12  -----(2)

(1) ⋅ 2  ==>  2x + 2y  =  10

(1) - (2)

2x + 2y - (2x + 3y)  =  10 - 12

-y  =  -2

y  =  2 (Number of tricycles)

So, there are two tricycles.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.