PSAT MATH PRACTICE

Question 1 :

If 8575  =  5^x ⋅ 7^y, what is (xy) - 5 ?

(A)  1  (B)  3  (C)  6  (D)  7  (E)  12

Solution :

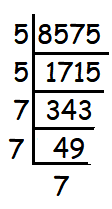
First, let us find the prime factors of 8575.

8575  =  5² ⋅ 7³

x = 2 and y = 3

xy - 5  =  2(3) - 5

  =  6 - 5

  =  1

Hence the answer is 1.

Question 2 :

When d is divided by 8, the remainder is 3. What is the remainder when d + 3 is divided by 8 ?

(A)  1  (B)  3  (C)  4  (D)  6  (E)  7

Solution :

Let d  =  11

Here we choose 11, because it is greater than 8, when we divide 11 by 8, we get the remainder 3.

Then d + 3  =  11 + 3  =  14

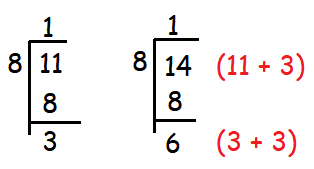
By dividing this d + 3 by 8, we get 6(3 + 3) as remainder.

Hence the answer is 6.

Note : The number chosen should be 3 more than the multiple of 8.

Question 3 :

Tommy is making as 6 letter password using only the letters A, B, C, D, E and F. How many different codes can Tommy make, if every letter can only be used once in each code ?

(A)  1  (B)  6  (C)  120  (D)  720  (E)  46, 656

Solution :

Let us mark 6 blank spaces.

____  ____  ____  ____  ____  ____

The first letter chosen be placed in any of the above 6 dashes.

Now, we have remaining 5 letters.

The second letter chosen, out of 5 may be placed in any one of the remaining 5 places.

In this way, we may create 6! codes by using 6 letters.

Hence the answer is 720.

Question 4 :

-5 (x -3) ≥ 20 what is the solution to the inequality shown above ?

(A)  x ≥ -1  (B)  x ≥ 7  (C)  x ≤ -1  (D)  x ≤ 7  (E)  x ≥ 1

Solution :

-5 (x -3) ≥ 20

-5x + 15  ≥ 20

Subtract 15 on both sides, we get 

-5x ≥ 20 - 15

-5x ≥ 5

Divide by -5 on both sides, we get

x ≤ -1

Question 5 :

Which numbers line below shows the solution to the inequality -2 < x/3 ≤ 2 ?

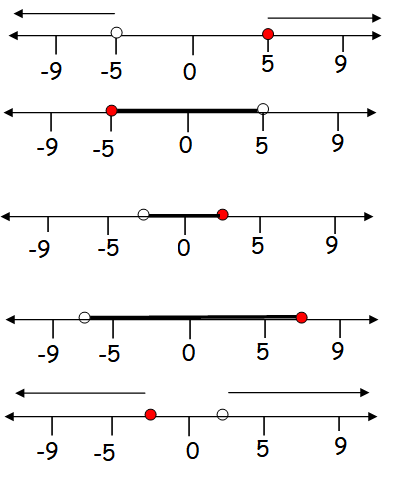
Solution :

  =  -2 < x/3 ≤ 2

Multiply the entire inequality by 3. So we get,

  =  -6 < x ≤ 6

The fourth option represents the the solution which is greater than -6 and less than or equal to 6.

Question 6 :

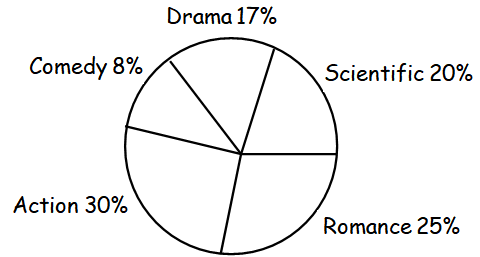
There are 15000 teens whose favorite genre is comedy. How many teens have a favorite genre of action ?

(A)  30  (B) 41,250  (C)  52,500

(D)  56,250  (E)  70,000

Solution :

Let "x" be the total population

8% of x  =  15000

0.08 x  =  15000

x  =  15000/0.08

x  =  187500

The number of teens whose genre is action 

  =  30% of 187500

  =  56250

Question 7 :

A computer originally prices at $550.50 is on sale for 20% off. Jamie used a 5% discount coupon which was applied to the sales price. How much did Jamie pay for the computer ?(Assume there is no tax)

(A)  $412.88  (B)  $418.38  (C)  $440.40

  (D)  $522.98  (E)  539.49

Solution :

Original price of computer  =  $550.50

From the 100% of price, the shop is going to give 20% off. Hence we have to pay 80% of the original price for the computer.

80% of 550.50  =  $440.40

Again we have 5% discount, so we have to calculate 95% of discounted price.

0.95 (440.40)  =  418.38

Hence the final amount for the computer is 418.38.

Question 8 :

Given the following value 4, 760 solve the following, x²/y, if x represents the smallest prime factor of the given value and y represents the greatest prime factor of the given value.

(A)  119/4  (B)  4/17  (C)  2/119   (D)  4/119  (E)  2/17

Solution :

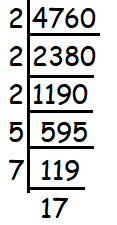
4760  =  2 ⋅ 2 ⋅ 2 ⋅ 5 ⋅ 7 ⋅ 17

Smallest prime factor  = 2, largest prime factor  =  17

  x²/y  =  2²/17  =  4/17

Hence the answer is 4/17.

Question 9 :

An adult male Diptera has a mass of 11.5 milligrams. What is the Diptera's mass in grams?

(A)  0.0115 g  (B)  0.115 g  (C)  1.15 g  

(D)  11.5 g  (E)  115 g

Solution :

1000 milli grams  =  1 gram

  =  (11.5/1000) grams

  =  0.0115 grams.

Question 10 :

Michel has a project due in exactly 83 hours. It is currently 8 : 30 on Monday morning. What time is his project due ?

(A)  6:30 PM Friday  (B)  7:30 PM Friday  

(C)  7:30 AM Thursday

(D)  7:30 PM Thursday  (E)  9:30 PM Thursday

Solution :

Every day consists of 24 hours. In 83 hours, we have three consecutive days and 11 hours remaining.

It is currently 8 : 30 on Monday morning. 

Then, we have

Monday (8:30 A.M) to Tuesday (8 : 30 A.M)  ==> 24 hours

Tuesday (8:30 A.M) to Wednesday (8 : 30 A.M)  ==> 24 hours

Wednesday (8:30 A.M) to Thursday (8 : 30 A.M)  ==> 24 hours

Thursday 8:30 A.M + 11 hours  =  Thursday 7.30 P.M. 

So, the project is due at 7.30 pm Thursday. 

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.