PROVING TRIANGLES ARE CONGRUENT WORKSHEET
Problem 1 :
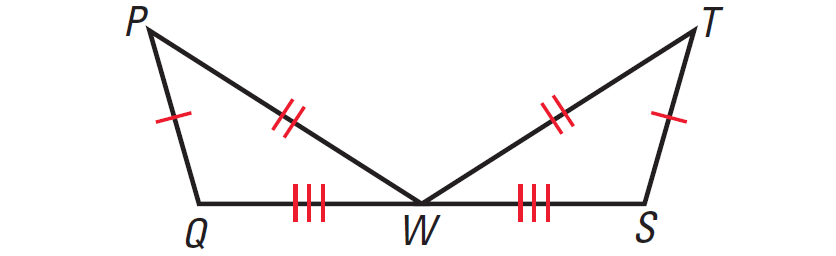
In the diagram given below, prove that ΔPQW ≅ ΔTSW.
Problem 2 :
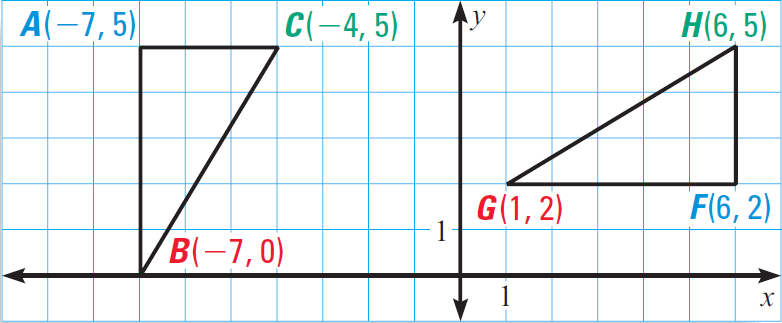
In the diagram given below, prove that ΔABC ≅ ΔFGH.
Problem 3 :
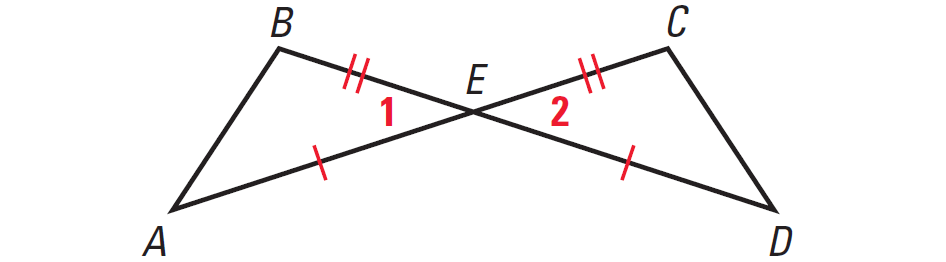
In the diagram given below, prove that ΔAEB ≅ ΔDEC.
Problem 4 :
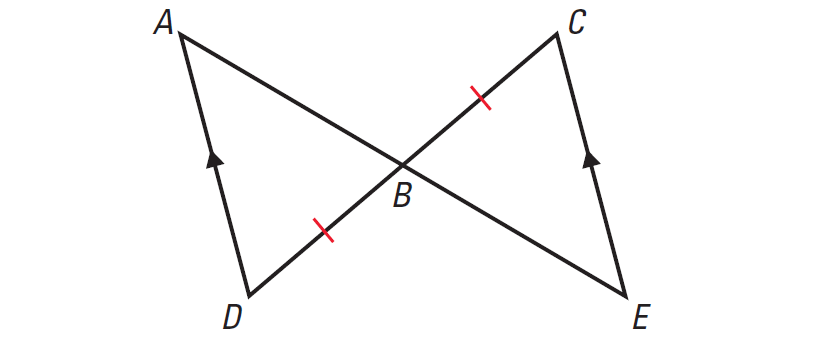
In the diagram given below, prove that ΔABD ≅ ΔEBC.
Problem 5 :
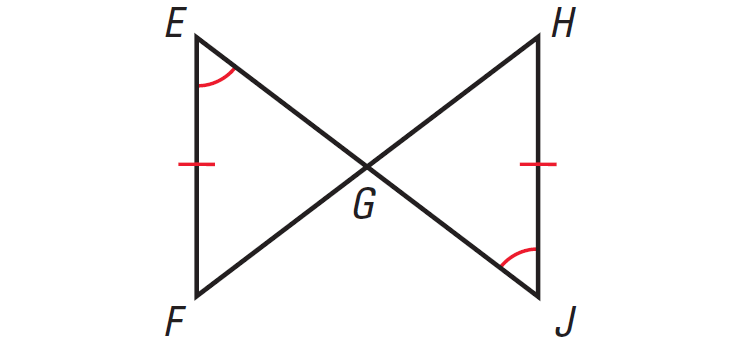
In the diagram given below, prove that ΔEFG ≅ ΔJHG.
Detailed Answer Key
Problem 1 :
In the diagram given below, prove that ΔPQW ≅ ΔTSW.
Solution :
|
Statements PQ ≅ ST PW ≅ TW QW ≅ SW ΔPQW ≅ ΔTSW |
Reasons Given Given Given SSS Congruence Postulate |
Problem 2 :
In the diagram given below, prove that ΔABC ≅ ΔFGH.
Solution :
Because AB = 5 in triangle ABC and FG = 5 in triangle FGH,
AB ≅ FG.
Because AC = 3 in triangle ABC and FH = 3 in triangle FGH,
AC ≅ FH.
Use the distance formula to find the lengths of BC and GH.
Length of BC :
BC = √[(x2 - x1)2 + (y2 - y1)2]
Here (x1, y1) = B(-7, 0) and (x2, y2) = C(-4, 5)
BC = √[(-4 + 7)2 + (5 - 0)2]
BC = √[32 + 52]
BC = √[9 + 25]
BC = √34
Length of GH :
GH = √[(x2 - x1)2 + (y2 - y1)2]
Here (x1, y1) = G(1, 2) and (x2, y2) = H(6, 5)
GH = √[(6 - 1)2 + (5 - 2)2]
GH = √[52 + 32]
GH = √[25 + 9]
GH = √34
Conclusion :
Because BC = √34 and GH = √34,
BC ≅ GH
All the three pairs of corresponding sides are congruent. By SSS congruence postulate,
ΔABC ≅ ΔFGH
Problem 3 :
In the diagram given below, prove that ΔAEB ≅ ΔDEC.
Solution :
|
Statements AE ≅ DE, BE ≅ CE ∠1 ≅ ∠2 ΔAEB ≅ ΔDEC |
Reasons Given Vertical Angles Theorem SAS Congruence Postulate |
Problem 4 :
In the diagram given below, prove that ΔABD ≅ ΔEBC.
|
Statements BD ≅ BC AD || EC ∠D ≅ ∠C ∠ABD ≅ ∠EBC ΔABD ≅ ΔEBC |
Reasons Given Given Alternate Interior Angles Theorem Vertical Angles Theorem ASA Congruence Postulate |
Problem 5 :
In the diagram given below, prove that ΔEFG ≅ ΔJHG.
|
Statements FE ≅ JH ∠E ≅ ∠J ∠EGF ≅ ∠JGH ΔEFG ≅ ΔJHG |
Reasons Given Given Vertical Angles Theorem AAS Congruence Postulate |
Apart from the stuff given above, if you need any other stuff in math, please use our google custom search here.
If you have any feedback about our math content, please mail us :
v4formath@gmail.com
We always appreciate your feedback.
You can also visit the following web pages on different stuff in math.
WORD PROBLEMS
Word problems on simple equations
Word problems on linear equations
Word problems on quadratic equations
Area and perimeter word problems
Word problems on direct variation and inverse variation
Word problems on comparing rates
Converting customary units word problems
Converting metric units word problems
Word problems on simple interest
Word problems on compound interest
Word problems on types of angles
Complementary and supplementary angles word problems
Trigonometry word problems
Markup and markdown word problems
Word problems on mixed fractrions
One step equation word problems
Linear inequalities word problems
Ratio and proportion word problems
Word problems on sets and venn diagrams
Pythagorean theorem word problems
Percent of a number word problems
Word problems on constant speed
Word problems on average speed
Word problems on sum of the angles of a triangle is 180 degree
OTHER TOPICS
Time, speed and distance shortcuts
Ratio and proportion shortcuts
Domain and range of rational functions
Domain and range of rational functions with holes
Graphing rational functions with holes
Converting repeating decimals in to fractions
Decimal representation of rational numbers
Finding square root using long division
L.C.M method to solve time and work problems
Translating the word problems in to algebraic expressions
Remainder when 2 power 256 is divided by 17
Remainder when 17 power 23 is divided by 16
Sum of all three digit numbers divisible by 6
Sum of all three digit numbers divisible by 7
Sum of all three digit numbers divisible by 8
Sum of all three digit numbers formed using 1, 3, 4
Sum of all three four digit numbers formed with non zero digits
Recent Articles
-
Properties of Radicals
Dec 08, 21 12:36 PM
Properties of Radicals
-
Properties of Radicals Worksheet
Dec 08, 21 12:32 PM
Properties of Radicals Worksheet
-
Properties of Square Roots Worksheet
Dec 08, 21 12:02 PM
Properties of Square Roots Worksheet
