PROVING TRIANGLE CONGRUENCE WORKSHEET

Problem 1 :

In the diagram given below, prove that ΔPQW  ≅  ΔTSW using two column proof.

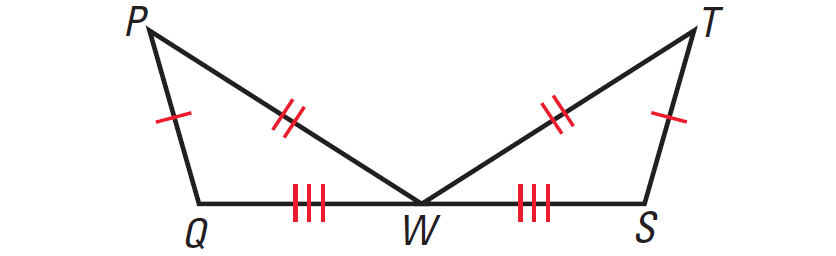
Problem 2 :

In the diagram given below, prove that ΔAEB ≅ ΔDEC using two column proof.

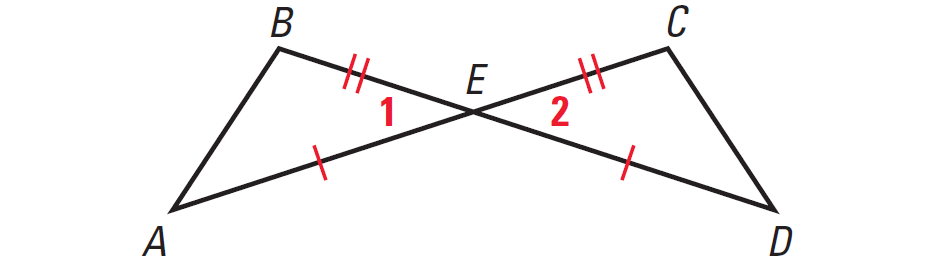
Problem 3 :

In the diagram given below, prove that ΔABD ≅ ΔEBC using two column proof.

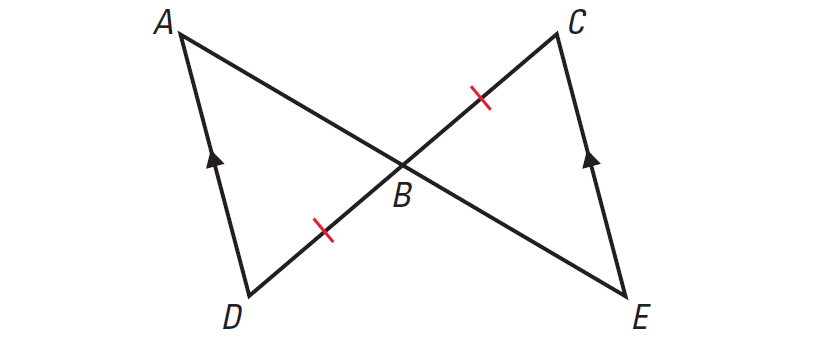
Problem 4 :

In the diagram given below, prove that ΔEFG ≅ ΔJHG using two column proof.

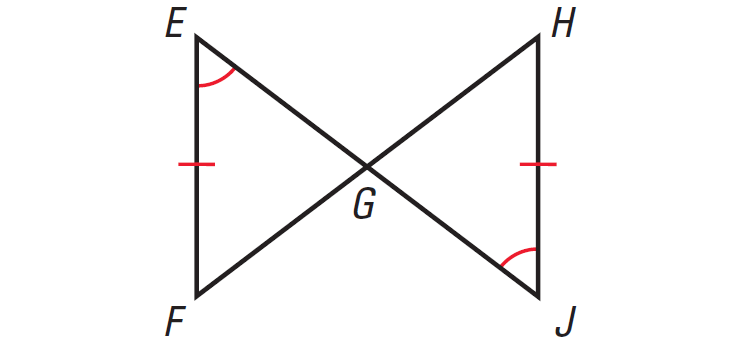
Problem 5 :

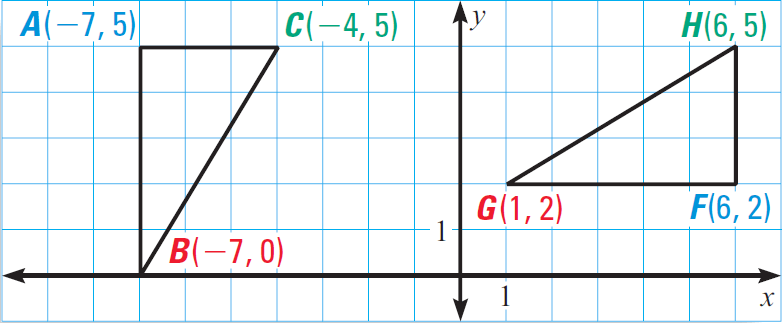
In the diagram given below, prove that ΔABC ≅ ΔFGH.

Problem 6 :

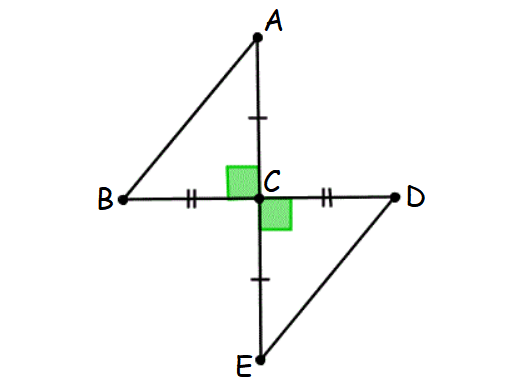
Check whether two triangles ABC and CDE are congruent.

Problem 7 :

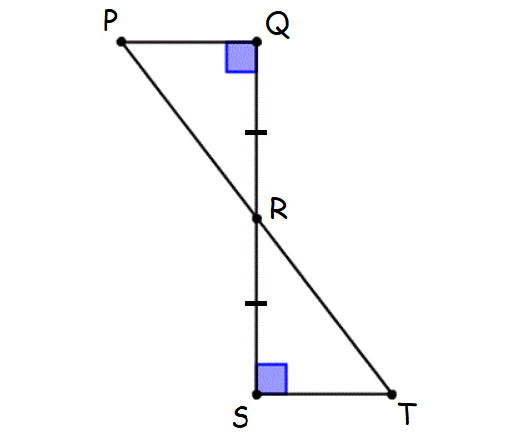
Check whether two triangles PQR and RST are congruent.

Problem 8 :

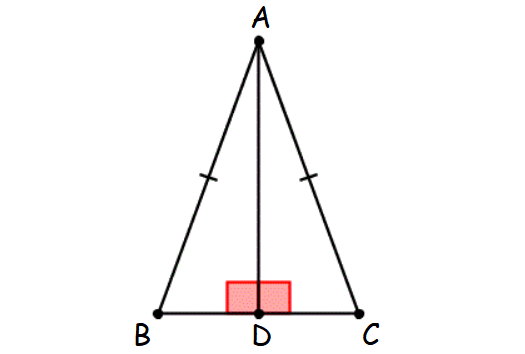
Check whether two triangles ABD and ACD are congruent.

1. Answer :

2. Answer :

3. Answer :

4. Answer :

5. Answer :

Because AB = 5 in triangle ABC and FG = 5 in triangle FGH,

AB ≅ FG

Because AC = 3 in triangle ABC and FH = 3 in triangle FGH,

AC ≅ FH

Use the distance formula to find the lengths of BC and GH.

Length of BC :

BC = √[(x₂ - x₁)² + (y₂ - y₁)²]

Here (x₁, x₁) = B(-7, 0) and (x₂, x₂) = C(-4, 5).

BC = √[(-4 + 7)² + (5 - 0)²]

= √[3² + 5²]

= √[9 + 25]

= √34

Length of GH : 

GH = √[(x₂ - x₁)² + (y₂ - y₁)²]

Here (x₁, x₁) = G(1, 2) and (x₂, x₂) = H(6, 5).

GH = √[(6 - 1)² + (5 - 2)²]

= √[5² + 3²]

= √[25 + 9]

= √34

Conclusion :

Because BC = √34 and GH = √34,

BC ≅ GH

All the three pairs of corresponding sides are congruent. By SSS congruence postulate,

ΔABC ≅ ΔFGH

6. Answer :

(i) Triangle ABC and triangle CDE are right triangles. Because they both have a right angle.

(i) AC = CE (Leg)

(ii) BC = CD (Leg)

Hence, the two triangles ABC and CDE are congruent by Leg-Leg theorem.

7. Answer :

(i) Triangle PQR and triangle RST are right triangles. Because they both have a right angle.

(ii) QR = RS (Given)

(iii) ∠PRQ = ∠SRT (Vertical Angles)

Hence, the two triangles PQR and RST are congruent by Leg-Acute (LA) Angle theorem.

8. Answer :

(i) Triangle ABD and triangle ACD are right triangles. Because they both have a right angle.

(i) AB = AC (Hypotenuse)

(ii) AD = AD (Common side, Leg)

Hence, the two triangles ABD and ACD are congruent by Hypotenuse-Leg (HL) theorem.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.