PROVING THE PYTHAGOREAN THEOREM

In a right triangle, the two sides that form the right angle are the legs. The side opposite the right angle is the hypotenuse.

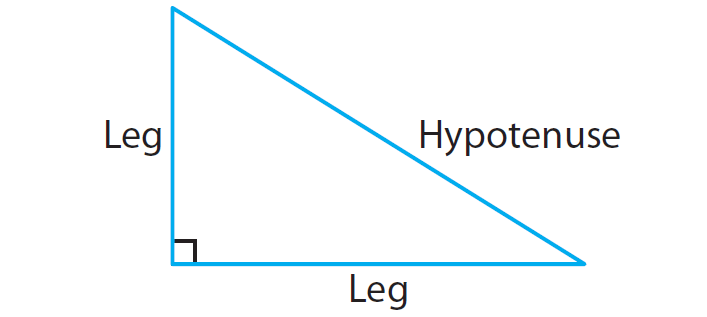
The Pythagorean Theorem

In a right triangle, the sum of the squares of the lengths of the  legs is equal to the square of the length of the hypotenuse.

If a and b are legs and c is the hypotenuse,

a² + b²  =  c²

Proving the Pythagorean Theorem

Step 1 :

Draw a right triangle on a piece of paper and cut it out. Make one leg shorter than the other.

Step 2 :

Trace your triangle onto another piece of paper four times, arranging them as shown. For each triangle, label the shorter leg a, the longer leg b, and the hypotenuse c.

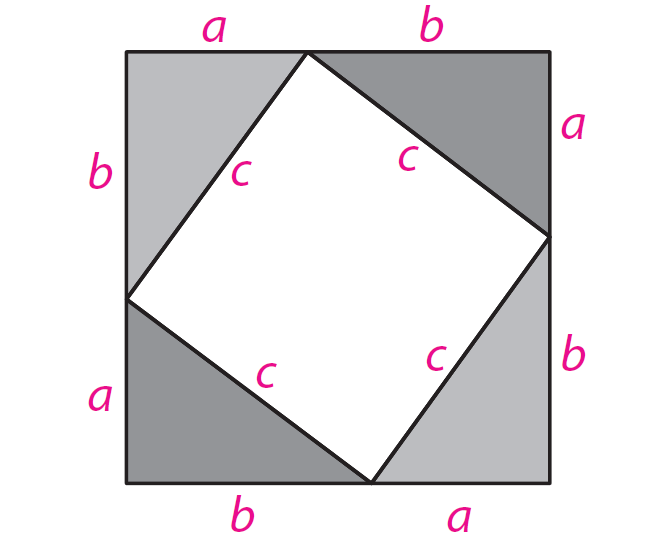
Step 3 :

Find the area of the unshaded square.

c² square units ----- (1)

Step 4 :

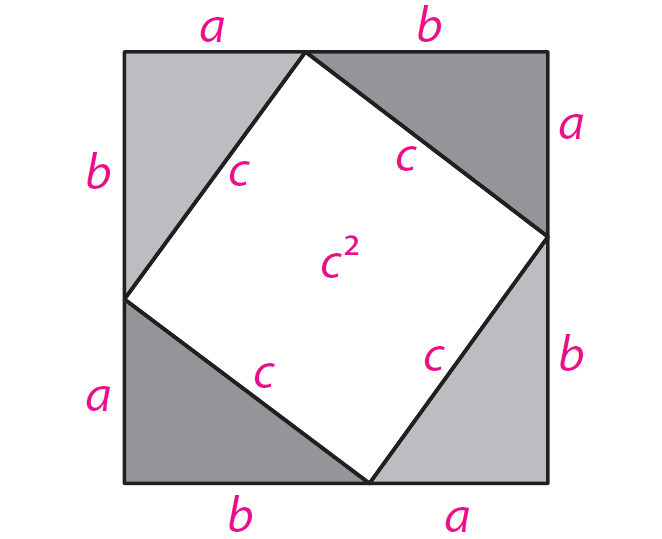
Label the unshaded square with its area.

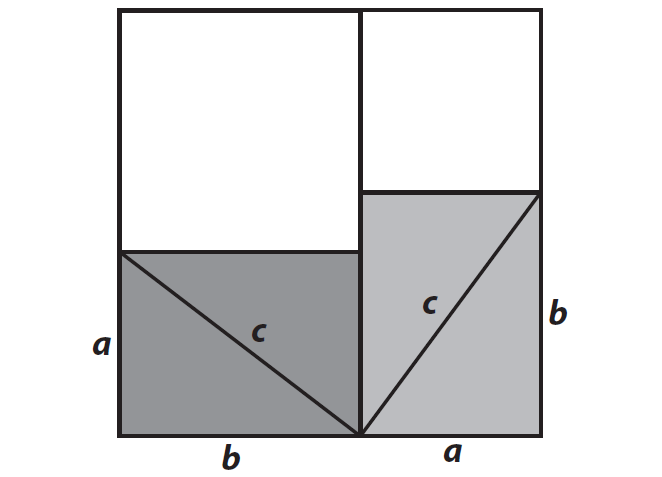
Step 5 :

Trace your original triangle onto a piece of paper four times again, arranging them as shown. Draw a line outlining a larger square that is the same size as the figure you made in step 2. 

Step 6 :

Find the area of the unshaded square at the top right and left of the figure in step 5.

a² square units and b² square units

Step 7 :

Label the unshaded squares with their areas.

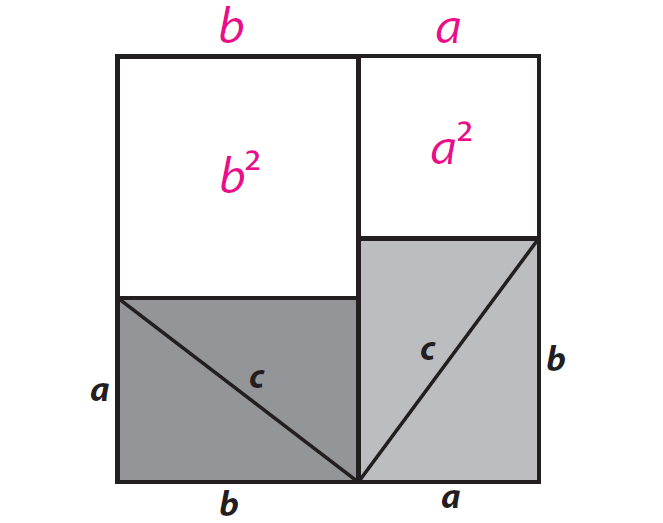
Step 8 :

Find the total area of the unshaded regions in step 5.

(a² + b²) square units -----(2)

Step 9 :

Because both (1) and (2) represent the total area of the unshaded region, they are equal.

So, we have

a² + b²  =  c²

Hence, the sum of the squares of the lengths of the  legs is equal to the square of the length of the hypotenuse.

Reflect

1. Explain whether the figures in step 2 and step 5 have the same area.

Yes, the figures in step 2 and step 5 have the same area. Because, the outlines of the figures are the same size.

2. Explain whether the unshaded regions of the figures in step 2 and step 5 have the same area.

Yes, the shaded regions have the same area. Subtracting the area of the shaded region from the total area gives the same area for the unshaded region in each figure.

3. Write an equation relating the area of the unshaded region in step 2 and step 5 have the same area.

a² + b²  =  c²

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.