PROVING THE PYTHAGOREAN THEOREM WORKSHEET

Problem 1 :

In the right triangle given below, prove the Pythagorean theorem. 

Problem 2 :

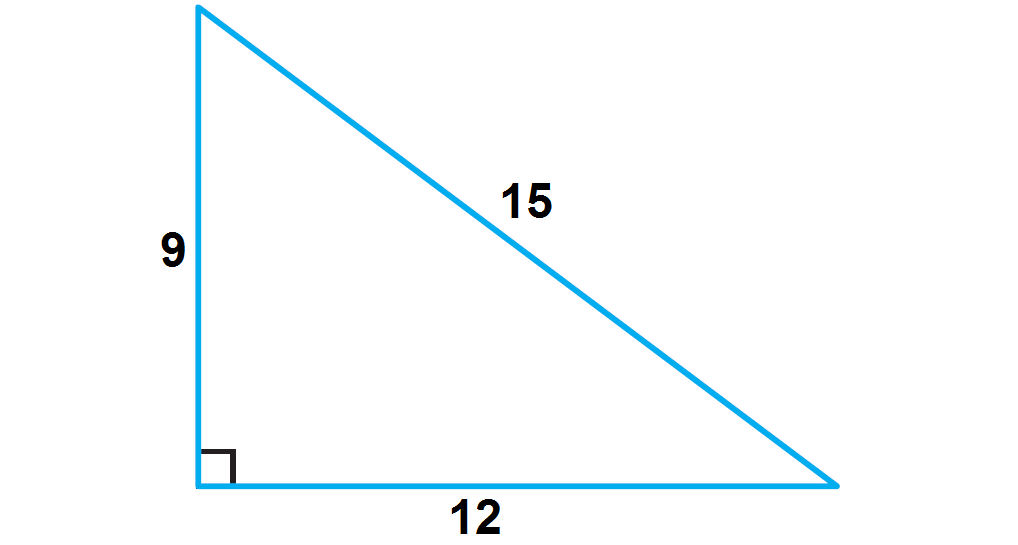
In the right triangle given below, prove the Pythagorean theorem. 

Problem 3 :

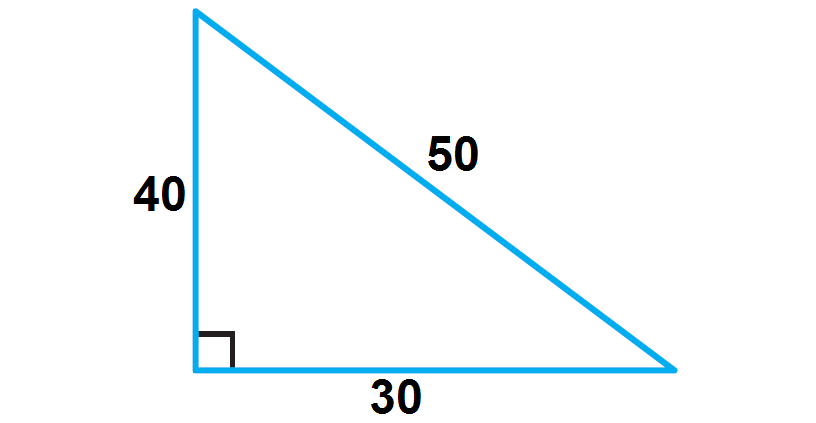
In the right triangle given below, prove the Pythagorean theorem. 

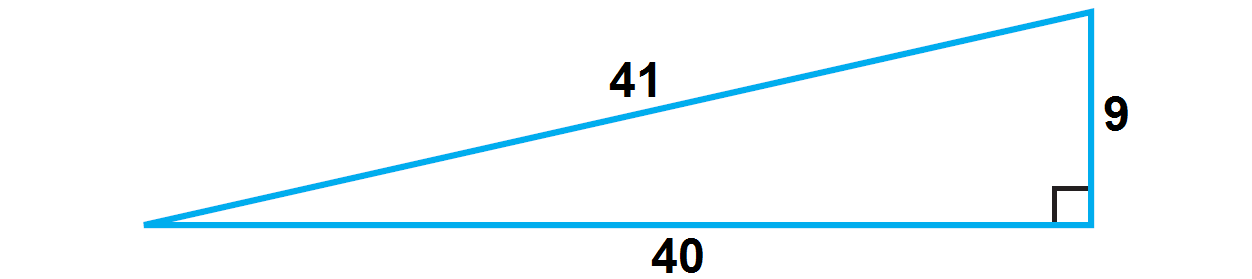
Problem 4 :

In the right triangle given below, prove the Pythagorean theorem. 

Answers

1. Answer :

Step 1 :

If a and b are legs and c is the hypotenuse, write Pythagorean for the above right triangle

a² + b²  =  c²

Step 2 :

In the above right triangle,

a  =  7, b  =  24 and c  =  25

Step 3 :

Find the value of a² + b² .

a² + b²  =  7² + 24²

a² + b²  =  49 + 576

a² + b²  =  625 -----(1)

Step 4 :

Find the value of c². 

c²  =  25²

c²  =  625 -----(2)

Step 5 :

From (1) and (2), we get

a² + b²  =  c²

2. Answer :

Step 1 :

If a and b are legs and c is the hypotenuse, write Pythagorean for the above right triangle

a² + b²  =  c²

Step 2 :

In the above right triangle,

a  =  9, b  =  12 and c  =  15

Step 3 :

Find the value of a² + b². 

a² + b²  =  9² + 12²

a² + b²  =  81 + 144

a² + b²  =  225 -----(1)

Step 4 :

Find the value of c². 

c²  =  15²

c²  =  225 -----(2)

Step 5 :

From (1) and (2), we get

a² + b²  =  c²

3. Answer :

Step 1 :

If a and b are legs and c is the hypotenuse, write Pythagorean for the above right triangle

a² + b²  =  c²

Step 2 :

In the above right triangle,

a  =  40, b  =  30 and c  =  50

Step 3 :

Find the value of a² + b². 

a² + b²  =  40² + 30²

a² + b²  =  1600 + 900

a² + b²  =  2500 -----(1)

Step 4 :

Find the value of c². 

c²  =  50²

c²  =  2500 -----(2)

Step 5 :

From (1) and (2), we get

a² + b²  =  c²

4. Answer :

Step 1 :

If a and b are legs and c is the hypotenuse, write Pythagorean for the above right triangle

a² + b²  =  c²

Step 2 :

In the above right triangle,

a  =  9, b  =  40 and c  =  41

Step 3 :

Find the value of a² + b². 

a² + b²  =  9² + 40²

a² + b²  =  81 + 1600

a² + b²  =  1681 -----(1)

Step 4 :

Find the value of c². 

c²  =  41²

c²  =  1681 -----(2)

Step 5 :

From (1) and (2), we get

a² + b²  =  c²

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.